Learning to Communicate

Learning to Communicate: The Emergence of Signaling in Spatialized Arrays of Neural Nets

Patrick Grim, Paul St. Denis, and Trina Kokalis

Group for Logic & Formal Semantics
Dept. of Philosophy
SUNY at Stony Brook
Stony Brook, NY 11794

patrick.grim@stonybrook.edu
(631) 632-7578
fax (631) 632-7522

Abstract:
We work with a large spatialized array of individuals in an environment of drifting food sources and predators. The behavior of each individual is generated by its simple neural net; individuals are capable of making one of two sounds and are capable of responding to sounds from their immediate neighbors by opening their mouths or hiding. An individual whose mouth is open in the presence of food is 'fed' and gains points; an individual who fails to hide when a predator is present is 'hurt' by losing points. Opening mouths, hiding, and making sounds each exact an energy cost. There is no direct evolutionary gain for acts of cooperation or 'successful communication' per se.

In such an environment we start with a spatialized array of neural nets with randomized weights. Using standard learning algorithms, our individuals 'train up' on the behavior of successful neighbors at regular intervals. Given that simple set-up, will a community of neural nets evolve a simple language for signaling the presence of food and predators? With important qualifications, the answer is 'yes'. In a simple spatial environment, pursuing individualistic gains and using partial training on successful neighbors, randomized neural nets can learn to communicate.

Keywords: communication, neural nets, learning, evolution, spatialization, philosophy of language

Shortened Title: Learning to Communicate

I. Introduction: The Philosophical Background

Philosophers have long been interested in meaning, but we believe they have often been hampered by the limits of their investigatory techniques. We think that modeling work on language and communication across a range of other disciplines, on the other hand, has sometimes been hampered by limited conceptual models for meaning.

Philosophers have typically relied on armchair reflection and linguistic intuition alone in developing theories of meaning, a source amplified only recently to include wider data from linguistics (Larson and Segal, 1995). One of our aims here is to offer computational modeling as an important addition to the toolkit for serious philosophy of language.

The limitations of modeling work across various disciplines due to limited conceptual models for meaning are somewhat more complicated. We offer a very rough sketch of alternative philosophical positions regarding meaning, both as a way of characterizing trends in contemporary research and in order to make clear the approach that motivates our work here. [1]

What is it for a sound or a gesture to have a meaning?

The classical approach has been to take meaning to be a relation. A sound or gesture is meaningful because it stands in a particular relation to something, and the thing to which it stands in the proper relation is taken to be its meaning. The question for any relational theory of meaning, then, is precisely what the crucial relation is and what it is a relation to.

One time-worn philosophical response is in terms of 'reference', taken as a relation to things in the world. Words have meanings because they have referents, and the meaning of a word is the thing to which it refers. In various forms such a theory of meaning can be found in Augustine (c. 400 AD), in Mill (1884), and in Russell (1921, 1940).

A second philosophical response is to consider meaning as a relation between a sound or gesture and the images, ideas, or internal representations it is used to express. On such a view the meaning of the word is that thing in the head it is used to convey. Communication becomes an attempt to transfer the contents of my head into yours, or to make the contents of your head match mine. An ideational theory of this sort can be found in Aristotle (c. 330 BC), Hobbes (1651), and Locke (1689), with a more sophisticated contemporary echo in Fodor (1975).

A third approach is to consider meaning as a relation neither to things in the world nor to the contents of heads but to some third form of object, removed from the world and yet non- psychological. Here a primary representative is Frege (1879).

It is our impression that relational theories of meaning are alive and well across the various disciplines involved in contemporary modeling regarding communication and language. The relational theory relied on is generally either referential or ideational; we take it as a sure sign that the theory in play is ideational when the measure of 'identity of meaning' or 'successful communication' is correspondence between individuals' representation maps or signal matrices. A referential theory, in which the meaning of a term is taken to be the object or situation it applies to, is more or less explicit in Batali (1995), Oliphant and Batali (1997), and MacLennan and Burghardt (1994). An ideational theory, in which communication involves a match of internal representations, is a clear theme in Levin (1995) and Parisi (1997); if activation levels of hidden nodes are taken as internal representations, Hutchins and Hazlehurst (1995) belong here as well. In modeling studies for language outside the immediate range of this paper we also find an ideational theory explicit in Livingstone and Fyfe (1999), Nowak, Krakauer and Dress (1999), Nowak, Plotkin, and Krakauer (1999), Nowak and Krakauer (1999), Livingstone (2000), and Nowak, Plotkin, and Jansen (2000).

Relational theories are not the only games in town, however. Much current philosophical work follows the intuition that variations on a Tarskian theory of truth can do much of the work traditionally expected of a theory of meaning (Quine 1960, Davidson 1967, Larson and Segal 1995). Of prime importance since the later Wittgenstein (1953) are also a class of theories which emphasize not meaning as something a word somehow has but communication as something that members of a community do. Wittgenstein is a notoriously hard man to interpret, but one clear theme is an insistence that meaning is to be understood not by looking for 'meanings' either in the world or in the head but by understanding the role of words and gestures in the action of agents within a community.

The emphasis on language as something used, and on significance as a property of use, continues in Austin (1962), Searle (1969), and Grice (1957, 1989). In Austin and Searle performative utterances such as 'I promise' take center stage, with the view that at least large aspects of meaning are to be understood by understanding an agent's actions with words. In Grice the key to meaning is the complicated pattern of intent and perceived intent on the part of speaker and listener.

We share with this last philosophical approach the conviction that a grasp of meaning will come not by looking for the right relation to the right kind of object but by attention to the coordinated interaction of agents in a community. In practical terms, the measure of communication will be functional coordination alone, rather than an attempt to find matches between internal representations or referential matrices. The understanding of meaning that we seek may thus come with an understanding of the development of patterns of functional communication within a community, but without our ever being able to identify a particular relation as the 'meaning' relation or a particular object concrete, ideational, or abstract as the 'meaning' of a particular term. [2] In applying tools of formal modeling within such an approach to meaning our most immediate philosophical precursors are Lewis (1969) and Skyrms (1996). Although the modeling literature may be dominated by relational views of meaning, this more dynamical approach also has its representatives: we note with satisfaction some comments in that direction in Hutchins and Hazelhurst (1995) and fairly explicit statements in Steels (1996, 1998).

Here an analogy may be helpful. We think that current misconceptions regarding meaning and the road to a more adequate understanding may parallel earlier misconceptions regarding another topic--biological life--and the road to a more adequate understanding there.

There was a time when life was thought of as some kind of component, quality, or even fluid that live bodies had and that dead bodies lacked. This is the picture that appears in the Biblical tradition of a 'breath of life', for example. As recently as Mary Shelley's Frankenstein (1831), life is portrayed as something that a live individual has and a dead individual lacks; in order to build a living being from dead parts one must somehow add the missing spark of life.

We now have a wonderful biological grasp of the phenomena of life, elegantly summarized for example in Dawkins' 'replicators' (Dawkins, 1976). But in our contemporary understanding life is not at all the kind of thing that Mary Shelley would have looked for. We understand life not as a magic component within individuals at a particular time but as a functional feature that characterizes a historical community of organisms evolving over time. Our understanding of life is also an understanding of something that may be continuous and a matter of degree: the question of precisely when in a history of evolving replicators the first creature counts as 'alive' is quite likely the wrong question.

Our conviction here, and the underlying philosophical motivation for the model we want to present, is that the same may be true of meaning. What we seek is a better understanding of the phenomena of meaning, which may come without any particular relation definable as the 'meaning relation' and even without identifiable 'meanings'. The proper way to understand meaning may be on the analogy of our current understanding of life; not as an all-or-nothing relation tying word to thing or idea, but as a complex continuum of properties characteristic of coordinated behavior within a community--a community of communicators--developing over time.

II. Modeling Background

Despite the complexity of this philosophical background, the model we have to offer is a very simple one.

We consider a large cellular automata array of individuals which gain points by 'feeding' and lose points when hit by a 'predator'. The cells themselves do not move, and thus have a fixed set of immediate neighbors in the array. Food sources and predators migrate in a random walk across the array, without being consumed or satiated. Thus a food source remains to continue its random walk even when a cell 'feeds' on it, and a predator continues its walk whether or not a cell has been victimized. When a food source lands on an individual whose mouth is open, that individual 'feeds' and gains points. When a predator lands on an individual that is not hiding, that individual is 'hurt' and loses points. Both mouth-opening and hiding, however, exact an energy cost.

Each of our individuals can also make one of two arbitrary sounds, heard only by itself and the eight cells touching it. In response to hearing such a sound, an individual might open its mouth, hide, do both or neither. But sound-making, like mouth-opening and hiding, exacts an energy cost.

Given this basic environment, one can envisage a community of 'communicators' which make sound 1 when fed, for example, and open their mouths when they hear sound 1 from themselves or any immediate neighbor. Since food sources migrate from cell to cell, such a pattern of behavior instantiated across a community would increase chances of feeding. A community of 'communicators' might also make sound 2 when hurt, and hide when they hear sound 2.

The individuals in our array are simple neural networks. The inputs to each net include whether the individual is fed on the current round, whether it is hurt, and any sounds heard from itself or any immediate neighbors. The net's outputs dictate whether the individual opens its mouth on the next round, whether it hides, and whether it makes either of two sounds. As noted, all rewards are in terms of food captured and predators avoided; there is no reward for communication per se.

Suppose we start with an array of neural nets with entirely randomized weights. Periodically, we have each of our individuals do a partial training on a sampling of the behavior of that neighbor that has amassed the most points. Changes in weights within individual nets follow standard learning algorithms, but learning is unsupervised in the traditional sense. There is no central supervisor or universal set of targets: learning proceeds purely locally, as individual nets do a partial training on the responses of those immediate neighbors that have proven most successful at a given time.

In such a context, might communities of 'communicators' emerge? With purely individual gains at issue, could a network of neural nets in this individualized environment nonetheless learn to communicate?

There are individual features that this model shares with particular predecessors. But there are also sharp contrasts with earlier models, and no previous model has all the characteristics we take to be important.

Most neural net models involving language have been models of idealized individuals. As is clear from the philosophical outline above, we on the contrary take communication to involve dynamic behavioral coordination across a community. We thus follow the general strategy of MacLennan and Burghardt (1994) and Hutchins and Hazelhurst (1995), emphasizing the community rather than the individual in building a model of language development. Luc Steels' (1998) outline of this shared perspective is particularly eloquent: Language may be

a mass phenomenon actualised by the different agents interacting with each other. No single individual has a complete view of the language nor does anyone control the language. In this sense, language is like a cloud of birds which attains and keeps its coherence based on individual rules enacted by each bird. (p. 384)

Another essential aspect of the model offered here is spatialization, carried over from our own previous work in both cooperation and simpler models for communication (Grim, 1995, 1996; Grim, Mar, and St. Denis, 1998; Grim, Kokalis, Tafti, and Kilb, 2000a; Grim, Kokalis, Tafti, and Kilb, 2000b). Our community is modeled as a two-dimensional torroidal or 'wrap- around' cellular automata array. Each individual interacts with its immediate neighbors, but no individual interacts with all members of the community as a whole. Our individuals are capable of making arbitrary sounds, but these are heard only by themselves and their immediate neighbors. Communication thus proceeds purely locally, regarding food sources and predators that migrate through the local area. Fitness is measured purely locally, and learning proceeds purely locally as well: individuals do a partial training, using standard algorithms, on that immediate neighbor that has proven most successful. Spatialization of this thorough-going sort has appeared only rarely in earlier modeling of communication. The tasks employed in Cangelosi and Parisi (1998), MacLennan and Burghardt (1994), and Wagner (2000) are in some sense conceived spatially, but both communication and reproduction proceed globally in each case across random selections from the population as a whole. Saunders and Pollack (1996) use a model in which a cooperative task and communication decay are conceived spatially, but in which new strategies arise by mutation using a fitness algorithm applied globally across the population as a whole. In Werner and Dyer (1991), blind 'males' and signaling 'females' are thought to find each other spatially, but random relocation of offspring results in an algorithm identical to a global breeding of those above a success threshold on a given task. Aside from our own previous work, Ackley and Littman (1994) is perhaps the most consistently spatialized model to date, with local communication and reproduction limited at least to breeding those individuals in a 'quad' with the highest fitness rating. Theirs is also a model complicated with a blizzard of further interacting factors, however, including reproductive 'festivals' and a peculiar wind-driven strategy diffusion.

We consider the individualistic reward structure of the model we offer here both more natural and more easily generalizable than many of its predecessors. In many previous models both 'senders' and 'receivers' are simultaneously rewarded in each case of 'successful communication', rather than rewards tracking natural benefits that can be expected to accrue to the receiver alone. An assumption of mutual benefit from communicative exchanges is explicitly made in the early theoretical outline offered by Lewis (1969). MacLennan (1991) offers a model in which both 'senders' and 'receivers' are both rewarded, with communicative strategies then perfected through the application of a genetic algorithm. As Ackley and Littman (1994) note, the result is an artificial environment "where 'truthful speech' by a speaker and 'right action' by a listener cause food to rain down on both" (40).

The work of MacLennan and Burghardt (1994), further developed in Wagner (2000), uses a genetic algorithm to modify a population of finite-state machines. Here again the structure is one in which both 'sender' and 'receiver' are mutually benefitted from 'successful communication.' In these studies a structure of symmetrical rewards is given a more plausible motivation, however: their work is explicitly limited to communication regarding cooperative activities in particular, motivated by a story of communication for cooperation in bringing down a large animal. That also limits the model's generalizability to communication in general, however. The same pattern of rewarding communicative 'matches' per se, rather than tracking the individual benefit that may or may not be gained from information communicated, reappears in the genetic algorithm work of Levin (1995).

Within neural net models in particular, symmetrical rewards for 'successful communication' characterize Werner and Dyer (1991), Saunders and Pollack (1996), and Hutchins and Hazelhurst (1995). In Werner and Dyer, using a genetic algorithm over (non- learning) neural nets, the topic is outlined as commmunication which facilitates reproduction by allowing 'males' and 'females' to find each other more rapidly, and thus benefits both sides of the 'communication' symmetrically. Saunders and Pollack (1996), using mutation on (non- learning) neural nets, employ a cooperative task in which each of two or three individuals is symmetrically rewarded if they manage jointly to consume an entire food supply. As do we, Hutchins and Hazelhurst (1995) study a community of interacting neural nets which change through learning rather than by mechanisms of mutation or genetic recombination, but their model is in other regards a puzzling one. Their five to fifteen nets are 'autoassociators,' training up individually on input configurations (twelve 'phases of the moon') as their target outputs. But the hidden layers of their nets are also labelled 'verbal input/output', and these hidden layers are trained directly on the hidden layers of other members drawn randomly from the population. Although Wagner (2000) criticizes the study on the grounds that "the meanings in their simulation have no connection to actions of the agents or states of a world in which the agents can take part--the meanings are arbitrary patterns chosen to study how a population of signalers can arrive at a consensus in their signaling" (p. 153), it is clear that Hutchins and Hazelhurst are in fact assuming a joint task that a common lexicon will facilitate. The target 'phases of the moon' appear in the earlier Hutchins and Hazelhurst (1991) correlated with tides, and the motivating story is one in which California Indians find it valuable to move the whole band to the beach to gather shellfish when and only when the tides are favorable. In the model itself it is thus a common lexicon per se that is trained toward, but this might have a connection to action where a cooperative task is at stake. Here as in the case of MacLennan and Burghardt (1994) and Wagner (2000), however, the model is then unsuitable for generalization to an environment in which individual receipt of information can be expected to be beneficial but the sending of information need not be.

The need for a model of how communication regarding non-shared tasks might originate is noted explicitly by Ackley and Littman (1994), Noble and Cliff (1996), Parisi (1997), Cangelosi and Parisi (1998), Dyer (1995), and Batali (1995). Batali writes:

While it is of clear benefit for the members of a population to be able to make use of information made available to others, it is not as obvious that any benefit accrues to the sender of informative signals. A good strategy, in fact, might be for an individual to exploit signals sent by others, but to send no informative signals itself. Thus there is a puzzle as to how coordinated systems of signal production and response could have evolved. (p. 2)

In an overview of various approaches, Parisi (1997) is still more explicit:

In the food and danger simulations the organism acts only as a receiver of signals and it evolves an ability to respond appropriately to these signals. It is interesting to ask,however, where these signals come from. . . Why should the second individual bother togenerate signals in the presence of the first individual? The evolutionary 'goal' of the first individual is quite clear. Individuals who respond to the signal 'food' ('danger') by approaching (avoiding) the object they currently perceive are more likely to reproduce than individuals who do not do so. Hence, the evolutionary emergence of an ability to understand these signals. . . But why should individuals who perceive food or danger objects in the presence of another individual develop a tendency to respond by emitting the signal 'food' or 'danger'? (129)

The model we offer here shows the emergence of a system of communication within a large community of neural nets using a structure of rewards that fits precisely the outline called for in Batali (1995) and Parisi (1997). Here individuals learn to communicate in an environment in which they benefit only from individual capture of food and avoidance of predators, and indeed in which there is an assigned cost for generating signals.

III. Preliminary Proto-nets

We structured our work as a series of progressively more developed models. Following that same pattern makes explanation simpler as well.

In those models with which we begin, the sample space of individuals is so small as to seem uninteresting and their structure is so simple that they are only a limiting case of neural networks: we term these simpler forms mere 'proto-nets'. The phenomenon of learning to communicate is nonetheless visible in even these proto-nets, and it is that basic phenomenon that we follow through the development of more complex models.

Our first array is a 64 x 64 torroidal or 'wrap-around' cellular automata grid, composed of a full 4096 individuals, but uses 200 food sources alone rather than (as later) both food sources and predators. On each round, each food source moves at random to one of 9 cells: that which it currently occupies or one of its 8 immediate neighbors. We think of these as food sources rather than individual food items because they continue their random walk without at any point being consumed or exhausted.

Our simple individuals have a behavior range that includes only opening their mouths on a given round or failing to do so; here there is no provision for hiding. If an individual has its mouth open on a round that a food item lands on it, it gains a point for 'feeding'. Any time it has its mouth open, it pays an 'energy tax' of .05 points. Thus an individual feeding gains .95 points, and an individual with its mouth open when no food is present loses .05. In this first simple format our individuals are also capable only of making one sound, heard by their immediate 8 neighbors and themselves. Making a sound also carries an 'energy tax' of .05 points.

The simplest aspect of this simple set-up, however, is the proto-nets which structure the behavior of our individuals. In our initial runs each individual has the elementary neural structure shown in Fig. 1. On each round, an individual has either heard a sound or it has not. This is coded as a bipolar +1 or -1. On each round, it has successfully fed on that round or has not, once again coded as a bipolar 1 or -1. Individuals' neural structures involve just two weights w1 and w2, each of which carries one of the following values: -3.5, -2.5, -1.5, -.5, +.5, +1.5, +2.5, +3.5. The bipolar input is multiplied by this weight on each side, and matched against a threshold of 0. If the weighted input is greater than 0 on the left side, the output is treated as +1 and the individual opens its mouth on the current round. If it is less than or equal to 0, the output is treated as -1 and the individual keeps its mouth closed. [3] If the weighted input is greater than 0 on the right side, the individual makes a sound heard by its immediate neighbors on the next round.

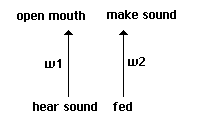
The elementary structure of our simplest proto-nets.
Fig. 1
We also add noise to this basic pattern for individual action. Because of lessons learned in earlier work regarding the necessity of 'imperfect worlds' in such a model of communication (Grim, Kokalis, Tafti, and Kilb, 2000a), we add an element of randomness: in a random 5% of all cases individuals will open their mouths whatever their input and weight assignments.

Our proto-nets are so simple as to lack not only hidden nodes but any branches with multiple inputs or outputs. Another element of simplicity is the fact that our weight values are at discrete 1.0 intervals. 'Chunked' or 'discrete' values of this type appear in earlier models with no learning algorithm (Werner and Dyer, 1991), but can also be used where the learning algorithm is a particularly simple one (Fausett, 1994; Plagianakos and Vrahatis, 1999).

With only two weights in the discrete intervals listed there are 64 possible weight combinations, but only four distinct behavioral strategies. An individual may either open its mouth when it hears a sound, or open its mouth when it does not: there is no provision for never opening its mouth, for example, or for constantly holding it open. The same applies to sound- making on the right side of the structure. Our four possible behaviors are thus the following:

We begin with a 64 x 64 array of individuals with randomized weights. After 100 rounds of food migration and individuals opening mouths and making sounds in terms of their randomized weights, some cells will have accumulated more points over all by capturing food and avoiding unnecessary mouth-openings.

At this stage, and after each 'century' of 100 rounds, each individual looks to see if it has an immediate neighbor with a higher score. If it does not, it maintains its current strategy. If it does have a more successful neighbor, it 'trains up' on that neighbor using a simple version of the delta rule with a learning rate of 1 (Fausett, 1994, 62ff.). In the case of a tie--two immediate neighbors with identical scores superior to that of a central cell--one neighbor is chosen randomly. A single training episode consists of picking a random pair of inputs for both the central cell and its most successful neighbor. If the outputs are the same, there is no change in the weights of the central cell. If the outputs are not the same, the relevant weight is nudged one unit in the direction that would have given it the appropriate answer. If a cell's response is positive for an input of -1 where its target neighbor's is negative, its weight w1 is moved one unit in the negative direction: from +2.5 to +1.5, for example. If a cell's response is negative for an input of -1 where its target neighbor's is positive, its weight w1 is moved one unit in the positive direction, perhaps from -1.5 to -0.5. The target response of the more successful neighbor, like our inputs, is recorded as a bipolar -1 or +1, allowing us to calculate the weight change for the central cell simply as w_new = w_old + (target input). The ends of our value scale are treated as absolute, however: no weight value is allowed to exceed +3.5 or fall below -3.5.

Despite the simplicity of our initial proto-nets, there is one behavioral strategy among our four that would clearly count as an elementary form of signaling or communication. A community of strategies following behavior 4 above would make a sound when they successfully fed, and that sound would be heard by themselves and their immediate neighbors. Those cells would open their mouths in response to hearing the sound, thereby increasing their chances of feeding on the following round (Fig. 2).

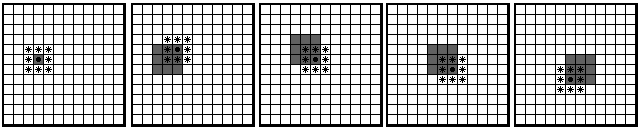
Migration of a single food source across a hypothetical array of communicators. In the left frame, a food source dot lands on an open mouth, indicated by gray shading. That central individual makes a sound * heard by itself and its immediate neighbors, which in the second frame open their mouths in response. One of them feeds successfully, making a sound heard by itself and its immediate neighbors, which are shown opening their mouths in the third frame. The result in a community of communicators is a chain reaction of efficient feeding.
Fig. 2
The question is whether communities of 'communicators' of this simple type will emerge by learning in our spatialized environment.

Such communities do indeed emerge. A typical progression is shown in the successive frames of Fig. 3, starting from an array of cells with randomized weights and proceeding to a field dominated by 'communicators' which eventually occupy the whole.

Learning to communicate in a field of four simple neural structures. Centuries 1-6 shown, with communicators in white and other strategies in shades of gray. Visual display of open mouths and sounding patterns omitted.
Fig. 3
For this simple model the progression to dominance by communicators is surprisingly fast. Figure 3 shows the first six centuries of a progression using 4 trainings (each using a single pair of random inputs) each century. Fig. 4 graphs behavioral strategies in terms of percentages of the total population over 15 centuries, using only a single training each century.

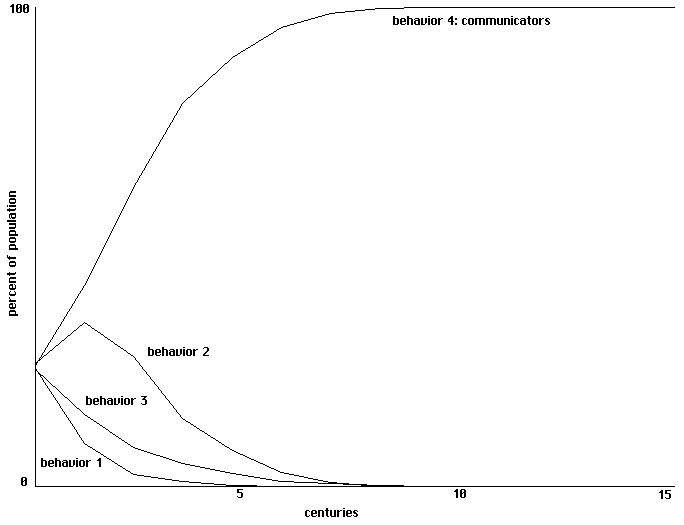
Learning to communicate in a field of 4 simple proto-nets, with 1 training each century. Percentages of the population for each behavior over 15 centuries.
Fig. 4
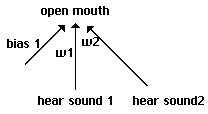
For a slightly more complicated model, we enrich our proto-nets with an added bias on each side, equivalent here to a settable threshold (Fig 5). Biases take the same weight range as w1 and w2, but are treated as having a constant +1 as input. The input -1 or +1 is multiplied by the weight and added to the bias; if this sum is greater than 0, the output is treated as +1 for an open mouth or a sound made.

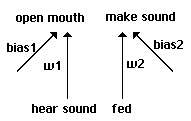
Proto-nets with biases.
Fig. 5
With biases added, each individual can be coded in terms of 4 weights, each between -3.5 and +3.5 at 1.0 intervals. This gives us 4096 numerically distinct strategies, and enlarges the number of possible behaviors to 16. An individual may never open its mouth, may open it only when it doesn't hear a sound, only when it does hear a sound, or may always keep it open. It may make a sound only when not fed, only when fed, it may always make a sound or it may never make a sound. The primary players in this model turn out to be the following:

Here as before we begin with a 64x64 torroidal array, randomizing weights and biases. Points for feeding and penalties for opening mouths and for making sounds are as before. Every 'century' of 100 rounds, individual cells train up in some determined number of runs on their most successful neighbor. For a response on a training run which differs from that of its more successful neighbor, the weights of a central cell are shifted one place toward what would have given it the correct response on that run, with biases shifted similarly. Within the limits of our value scale, w_new = w_old + (target x input) and bias_new = bias_old + target.

In this slightly more complicated model it is clearly behavior 11 that is the 'communicator', responding to a heard sound by opening its mouth and making a sound only when fed. Will communities of this particular behavioral strategy develop through learning?

Figure 6 uses percentage of population to show conquest by communication over 65 centuries with a single training each century. For 2 trainings conquest by communicators may take 40 centuries, while for 4 trainings conquest can occur in as few as 22 centuries, but the over-all pattern is otherwise similar. In each case those behavioral strategies other than communicators that do the best are variants which benefit from receipt of information from communicators but follow some different pattern of sounding in return. The second highest curve in each case is that of behavior 10, which opens its mouth only when it hears a sound, as do communicators, but makes a sound only when not fed. The third highest curve in each case is that of behavior 9, which opens its mouth when it hears a sound but never itself makes any sound in return.

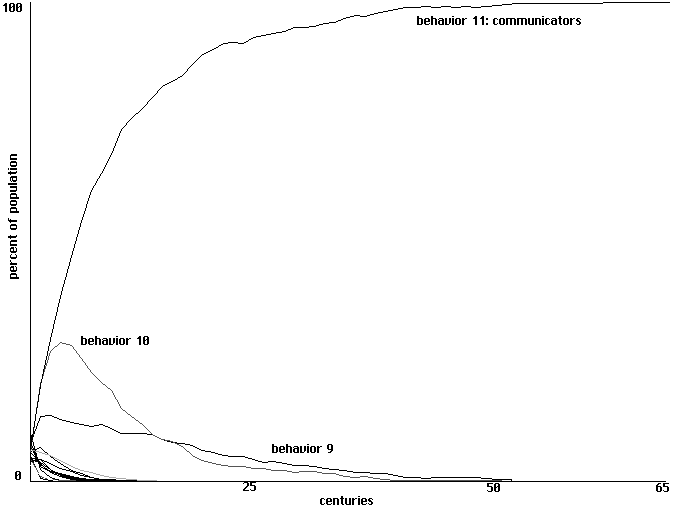
Learning to communicate in a field of 16 proto-nets, with 1 training each century. Percentages of the population shown over 65 centuries.
Fig. 6
IV. Learning to Communicate in an Array of Perceptrons

In the spatialized environment of the preceding section, communities of communicators arise through the learning mechanisms of a simple version of the delta rule. There our neural structures are so simple as to qualify only as limiting cases of neural networks, however, and the sample space from which communicative strategies emerge is correspondingly small.

Here we offer a more developed form of the model, in which the environment is enriched to contain the threat of predators as well as the promise of food sources. The behavioral repertoire of each cell is wider as well: on a given round each individual (1) can open its mouth, gaining points if food lands on it, and (2) it can hide, which will keep it from losing points if a predator lands on it. Opening one's mouth and hiding each carry an energy expenditure of .05 points. An individual can also avoid energy expenditure by occupying a neutral stance in which it neither opens its mouth nor hides, gaining no points if food is present but still open to harm from predators. Our neutral structure is such that it is also possible for a cell to both hide and have its mouth open on a given turn, gaining the advantage of each but paying a double energy expenditure.

In this model each individual has two arbitrary sounds it can make, heard by its immediate neighbors and itself, and it can react in different ways to sounds heard. Making a sound also carries an energy expenditure of .05 points.

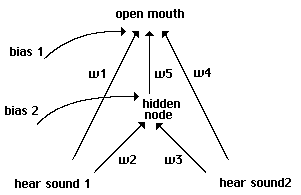
Here our individuals employ full neural nets, though with no hidden layers: the behavior of each individual is generated by a two-layer perceptron. We begin with neural nets using fixed thresholds and without biases, as shown in Fig. 7. Each of the 4096 individuals in our 64 x 64 array is now coded in terms of 8 weights, each of which takes a value between -3.5 and +3.5 at 1.0 intervals as before. The basic neural component of our nets is shown in Fig. 8. The structure of this 'quadrant' is repeated four times in the complete structure shown in Fig. 7, with two quadrants sharing inputs in each of two 'lobes'.

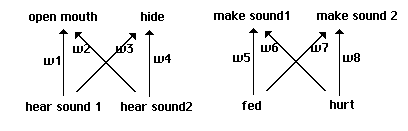
Neural structure of initial perceptrons.
Fig. 7

The basic neural structure of each quadrant.
Fig. 8
We use a bipolar coding for inputs, so that 'hear sound 1' takes a value of +1 if the individual hears sound 1 from any immediate neighbor or itself on the previous round. It takes a value of -1 if the individual does not hear sound 1. Each input is multiplied by the weight shown on arrows from it, and the weighted inputs are then summed at the output node. If that total is greater than 0, we take our output to be +1, and the individual opens its mouth, for example; if the weighted total is less than or equal to 0, we take our output to be -1, and the individual keeps its mouth closed. Here as throughout an element of 'noise' is also built in: in a random 5% of cases each individual will open its mouth regardless of weights and inputs. On the other side of the lobe, individuals also hide in a random 5% of cases.

There are four possible sets of inputs for each quadrant: (-1, -1), (-1, +1), (+1, -1), and (+1, +1). In principle, the output in each case might be either 1 or +1, giving us the standard 16 Boolean functions. But not all net architectures can represent all 16 Booleans, and it is well known that perceptrons are limited in this regard (Minsky and Papert, 1990). For the current structure, with bipolar inputs, two weights, and a simple 0 threshold, there are in fact only 8 outputs possible for each quadrant. An individual's structure may be such that it opens its mouth, for example, under any of the following input specifications:

With 8 behavioral possibilities for each of the four quadrants of the network, we have a space of 4096 possible behavioral strategies.

We initially populate our array with neural nets carrying eight random weights. 100 food sources and 200 predators drift in a random walk across the array, without at any point being consumed or satiated. [4] Although very rare, it is possible for a food source and a predator to occupy the same space at the same time. Whenever a cell has its mouth open and a food source lands on it, it feeds and gains 1 point. Whenever a predator lands on a cell that is not hiding, that cell is 'hurt' and loses 1 point. Over the course of 100 rounds, our individuals total their points as before. They then scan their 8 immediate neighbors to see if any has garnered a higher score. If so, they do a partial training on the behavior of their highest-scoring neighbor.

Here again we use the simple variation of the delta rule as our training algorithm. For a set of four random inputs, the cell compares its outputs with those of its higher-scoring neighbor. At any point at which those differ, it nudges each of the responsible weights one unit positively or negatively. Within the limits of our value scale, w_new = w_old + (target input). Where outputs are the same for a cell and its target for a given set of inputs, no change is made.

In the current model, we use a training run of four random sets of inputs with no provision against duplication. If a cell has a neighbor with a higher score, in other words, it compares its behavior with that of its neighbor over four random sets of inputs, changing weights where there is a difference. Training will thus clearly be partial: only four sets of inputs are sampled, rather than the full 16 possible, and indeed the same set may be sampled repeatedly. The learning algorithm is applied using each set of inputs only once, moreover, leaving no guarantee that each weight is shifted enough to make the behavioral difference that would be observable in a complete training. The idea of partial training was quite deliberately built into our model in order to allow numerical combinations and behavioral strategies to emerge from training which might not previously have existed in either teacher or learner, thereby allowing a wider exploration of the sample space of possible strategies. In all but one of the runs illustrated below, for example, there are no 'perfect communicator' cells in our initial randomizations; those strategies are 'discovered' by the mechanics of partial training. [5]

From Fig. 7 it is clear that the neural architecture used here divides into two distinct halves: a right half that reacts to being fed or hurt by making sounds, and a left half that reacts to sounds heard by opening its mouth or hiding. No feed-forward connection goes from hearing sounds, for example, directly to making sounds. With an eye to keeping variables as few as possible in a population of thousands of individuals, we found no need to complicate the model by connections between the two sides.

This 'two lobe' configuration of communication seems to have been re-invented or re- discovered repeatedly in the history of the literature. Many note an intrinsic distinction between the kinds of action represented here by (1) making sounds and (2) mouth-opening or hiding in response to sounds heard. MacLennan (1991) similarly distinguishes 'emissions' from 'actions', for example, and Oliphant and Batali (1997) distinguish 'transmission behavior' from 'reception behavior.' It also seems natural to embody that distinction in the neural architecture of the individuals modelled: Werner and Dyer (1991) separate precisely these two functions between two different sexes, Cangelosi and Parisi (1998) note that the architecture of their neural nets uses two separate sets of connection weights for the two kinds of action, and Martin Nowak notes that his active matrix for signal-sending and his passive matrix for signal-reading can be treated as completely independent (Nowak, Plotkin, and Krakauer, 1999; Nowak, Plotkin, and Jansen, 2000). It is clear that such a structure builds in no presumption that individuals will treat signals as bi-directional in the sense of de Saussure (1916): that a signal will be read in the same way that it is sent. If bi-directionality nonetheless emerges, as indeed it does in our communities of 'communicators', it will be as a consequence not of a structural constraint but of learning in an environment (see also Oliphant and Batali, 1997).

We start with an array of neural nets with randomized weights. Of our 4096 behavioral strategies, only two count as 'perfect communicators'. One of these generates a sound 1 when fed and a sound 2 when hurt, responding symmetrically to sound 1 by opening its mouth and to sound 2 by hiding. The behavior of the other 'perfect communicator' is the same with the role of sounds 1 and 2 reversed. With a sample space of 4096 behavioral strategies and a learning algorithm in which individual cells do a partial training on their most successful neighbor, will communities of these communicators emerge?

The answer is yes. Fig. 9 shows a typical run of 200 centuries with a clear emergence of our two perfect communicators. Given our limited number of strategies, there were a small number of perfect communicators in this initial randomization. When re-run with an initial randomization that eliminated all perfect communicators, however, the long-range results were essentially identical.

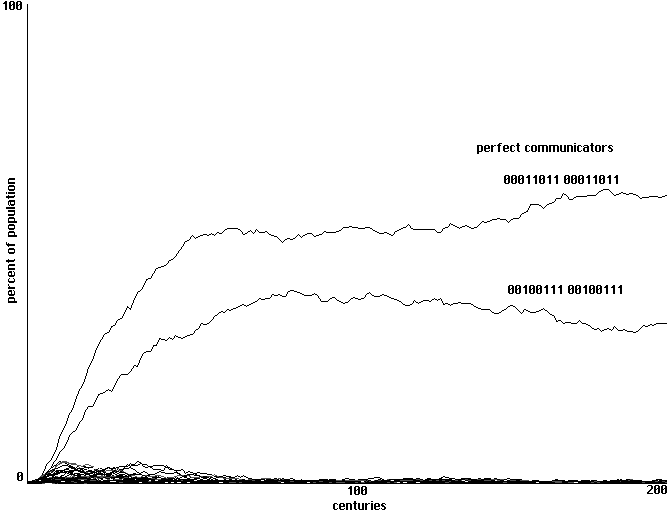
Learning to communicate in a field ofd perceptrons: emergence of two forms of perfect communicators within a sample space of 4096 strategies. 4 training runs each century, 200 centuries shown.
Fig. 9
As noted, each of the four quadrants of the neural nets used here can generate a behavior corresponding to only 8 of the 16 possible Boolean functions. We can complicate our networks by the addition of biases, however, giving them the structure for each quadrant shown in Fig. 10. With that addition our quadrants will be able to represent 14 of the 16 Booleans. The two Booleans that can not be captured within such a structure are exclusive 'or' and the biconditional. Such a net has no way of giving an output just in case (Xor) either sound 1 is heard or sound 2 is heard, but not both, for example, or just in case (Bicond) either both are heard or neither is heard. For present purposes these unrepresented Boolean connectives are at the periphery of functions that might plausibly be selected by the environmental pressures in the model, however, and the failure to capture them seems a minor limitation. We leave further pursuit of the full range of the Booleans to the following section.

Perceptron quadrants with biases.
Fig. 10

The complete perceptron architecture with biases.
Fig. 11
As a whole, our perceptrons use 12 weights, including biases, and take the form shown in Fig. 11. With a total of 12 chunked weights, we can represent 14 of 16 Boolean functions in each quadrant and enlarge our sample space from 4096 to 38,416 behavioral strategies. We code these behavioral strategies in terms of outputs for different pairs of inputs. The possible inputs at 'hear sound 1' and 'hear sound 2' for the left 'lobe' of our structure are (-1,-1), (-1, +1), (+1, -1), and (+1, +1). Outputs for a given strategy will be pairs representing the output values for 'open mouth' and 'hide' for each of these pairs of inputs. We might thus encode the left-lobe behavior of a given strategy as a series of 8 binary digits. The string 00 00 00 11, for example, represents a behavior that outputs an open mouth or a hide only if both sounds are heard, and then outputs both. The string 00 01 01 01 characterizes a cell that never opens its mouth, but hides if it hears either sound or both. We can use a similar pattern of behavioral coding for the right lobe, and thus encode the entire behavior of a net with 16 binary digits. We will standardly represent the behavior for a complete net using a single separation between the two lobes, as in 00110011 11001100.

Of the 38,416 behavioral strategies in our sample space, there are still only two that qualify as 'perfect communicators'. Pattern 00011011 00011011 represents an individual that hides whenever it hears sound 2, eats whenever it hears sound 1, makes sound 2 whenever it is hurt and makes sound 1 whenever it is fed. The 'whenever' indicates that it will both hide and open its mouth when it hears both sounds and will make both sounds when both hurt and fed. The pattern 00100111 00100111 represents an individual with a symmetrical behavior in which only the sound-correlations are changed: it reacts to sound 2 by eating and responds to being fed by making sound 2, reacts to sound 1 by hiding and responds to being hurt by making sound 1.

Will random arrays of perceptrons in this larger sample space of strategies learn to form communities of communicators?

Here again the answer is yes. Fig. 12 shows an emergence of communication in 300 centuries. Our initial array contains no perfect communicators. One appears in the second century; the other appears in the seventh, disappears in the eighth, and is re-discovered in the ninth. As they proliferate, the two versions of perfect communicator form spatially distinct communities, separated at their interface by a shifting border of strategies attempting to negotiate between the two language communities. Century 290 of this development is shown in Fig. 13. [6]

Learning to communicate in a randomized array of perceptrons and a sample space of 38,416 behavioral strategies. 300 centuries shown.
Fig. 12

Communities of two perfect communicators at century 290, shown in pure black and pure white.
Fig. 13
V. Learning to Communicate using Backpropagation in an Array of Neural Nets

It has long been known that a neural net of just two layers is incapable of representing all of the Boolean functions: we've noted the exclusive 'or' and biconditional as exceptions. This crucial limitation dulls the impact of the otherwise remarkable perceptron learning convergence theorem: that the simple delta rule is adequate to train any perceptron, in a finite number of steps, to any function it can represent (Rosenblatt 1959, 1962; Minsky and Papert, 1990; Fausett 1994). Historically, this limitation posed a significant stumbling block to the further development of neural nets in the 1970s. It was known even then that the addition of intermediate layers to perceptrons would result in multiple layer neural nets which could model the full spectrum of Boolean functions, but the simple delta rule was known to be inadequate for training multiple-layer nets.

With the use of continuous and differentiable activation functions, however, multiple- layer neural nets can be trained by backpropagation of errors using a generalized delta function. This discovery signaled the re-emergence of active research on neural nets in the 1980s (McClelland and Rumelhart, 1988). Here again there is a convergence theorem: it can be shown that any continuous mapping can be approximated to any arbitrary accuracy by using backpropagation on a net with some number of neurons in a single hidden layer (White, 1990; Fausett, 1994).

The most complicated neural nets we have to offer here exploit backpropagation techniques in order to train to the full range of Boolean functions of their inputs. Each of our nets is again divided into two 'lobes,' with inputs of two different sounds on the left side and outputs of mouth-opening or hiding, inputs of 'fed' and 'hurt' on the right side with outputs of two different sounds made. Each of these lobes is again divided into two quadrants, but our quadrants are now structured as neural nets with a single hidden node (Fig. 14).

The quadrant structure of our backpropagation nets.
Fig. 14
The feedforward neural nets most commonly illustrated in the literature have hierarchically uniform levels all inputs feed to a hidden layer, for example, and only the hidden layer feeds to output. For reasons of economy in the number of nodes and weights to be carried in memory over a large array of neural nets, the design of our nets is not hierarchically uniform. As is clear from Fig. 14, inputs feed through weights w1 and w4 directly to the output node as well as through weights w2 and w3 to a hidden node. The output node receives signals both from inputs directly and through weight w5 from the hidden node.

At both the hidden mode and the output mode we use a sigmoid activation function f(x) = (>2 / [1 + exp(-x)]) - 1 equivalent to [1 - exp(-x)] / [1 + exp(-x)] , graphed in Fig. 15. In our sample quadrant, bipolar inputs -1 or +1 from 'hear sound 1' and 'hear sound 2' are first multiplied by weights w2 and w3, initially set between -3.5 and +3.5. At the hidden node, those products are added to a constant bias 2 set initially in the same range. The total is then treated as input to the activation function above, generating an output somewhere between -1 and +1 that is sent down the line to the output node.

Activation function.
Fig. 15
The signal from the hidden node is multiplied by weight w5, which is added at the output node to the product of the initial inputs times weights w1 and w4. Bias 1 is also added to the sum. Here again all initial weights and biases are set between -3.5 and +3.5. This output is again passed through our activation function, with final output >0 treated as a signal to open the mouth, for example, and an output < 0 as not opening the mouth. With different weight settings, this simple multi-layered structure is adequate to represent all 16 Boolean functions.

The training algorithm, appropriate to nets with this structure, [7] can be illustrated in terms of the single quadrant in Fig. 15. We operate our net feedforward to obtain a final output o of -1 or +1. We calculate an output error information term d_o = (t - o) in terms of o and our target t. d_o is applied directly to calculate changes in weights w1 and w4 on lines feeding straight from inputs. With a learning rate lr set at .02 throughout, Dw1 = lr x d_o input(sound 1), with a similar calculation for w4 and bias 1. The weight change for w5 is calculated in terms of the signal which was sent down the line from hidden to output node in the feedforward operation of the net: Dw5 = lr x d_o x output(h) .

Weight changes for w2 and w3 are calculated by backpropagation. We calculate an error information term dh = w5 x d_o x f ' (inp_h), where f ' (inp_h) is the derivative of our activation function applied to the sum of weighted inputs at our hidden node. Changes in weights w2 and w3 are then calculated in terms of d_h and our initial inputs: Dw2 = lr x d_h x input(sound 1), with a similar treatment for w3 and bias 2. Once all weight and bias changes are calculated, they are simultaneously put into play: w_new = w_old + Dw for each of our weights and biases.

We wanted to assure ourselves that our net structure was satisfactorily trainable to the full range of Booleans. The convergence theorem for standard backpropagation on multiple- layered and hierarchically uniform neural nets shows that a neural net with a sufficient number of nodes in a hidden layer can be trained to approximate any continuous function to any arbitrary accuracy (White 1990; Fausett 1994). Our nets are not hierarchically uniform, however, they employ only a single hidden node, and our training is to the Booleans rather than a continuous function. Is the training algorithm outlined here adequate to the task?

With minor qualification, the answer is 'yes'. We ran groups of 4000 initial random sets of weights in the interval between -3.5 and +3.5 for a quadrant of our net. Training for each set of weights was to each of the 16 Boolean functions, giving 64,000 training tests. Trainings were measured in terms of 'epochs', sets of all possible input configurations in a randomized order. Our results showed successful training to require an average of 16 epochs, though in a set of 64,000 training tests there were on average approximately 6 tests, or .01%, in which a particular weight set would not train to a particular Boolean in less than 3000 epochs. [8] As those familiar with practical application of neural nets are aware, some weight sets simply 'don't train well.' The algorithm outlined did prove adequate for training in 99.99% of cases involving random initial weight sets and arbitrary Booleans.

For the sake of simplicity we have outlined the basic structure of our nets and our training algorithm above in terms of an isolated quadrant. Our nets as a whole are four times as complicated, of course, with two lobes of two quadrants each (Fig. 16).

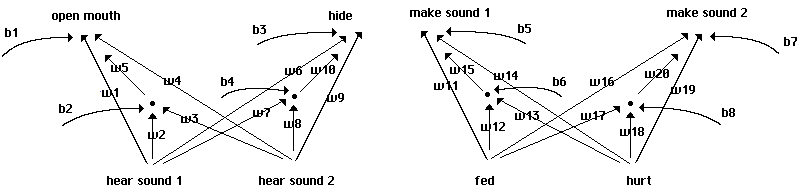
The full architecture of our neural nets.
Fig. 16
Each of our neural nets employs a total of 20 weights, plus eight biases, requiring a total of 28 variable specifications for each net at a given time. In the networks of previous sections, we used discrete values for our weights: weights could take on values only at 1.0 intervals between -3.5 and +3.5. For the simple learning rule used there this was a useful simplification. Backpropagation, however, demands a continuous and differentiable activation function, and will not work properly with these 'chunked' approximations. Here, therefore, our individual nets are specified at any time in terms of 28 real values in the range between -3.5 and +3.5. Each quadrant is capable of 16 different output patterns for a complete cycle of possible inputs, and our sample space is expanded to 65,536 distinct behavioral strategies.

Here as before we can code our behavioral strategies in terms of binary strings. Pairs of digits such as 01 represent a lobe's output for a single pair of inputs. A coding 00 01 01 11 can thus be used to represent output over all possible pairs of inputs to a lobe: (-1,-1), (-1, +1), (+1, -1), and (+1, +1). A double set 01111000 00100011 serves to represent the behavior of both lobes in a network as a whole.

Of the 65,536 behavioral strategies that can thus be encoded, there are precisely two that qualify as 'perfect communicators'. The pattern 00011011 00011011 represents and individual that makes sound 1 whenever it is fed and reacts to sound 1 by opening its mouth, makes sound 2 whenever it is hurt and reacts to sound 2 by hiding. It will both hide and open its mouth when it hears both sounds and will make both sounds when both hurt and fed. Pattern 00100111 00100111 represents an individual with a symmetrical behavior in which only the sound correlations are changed. This second individual makes sound 2 when it is fed and reacts to sound 2 by opening its mouth, makes sound 1 when hurt and reacts to sound 1 by hiding.

There are also variants on the pattern of perfect communicators that differ by a single digit in their encoding. Those that play the most significant role in runs such as those below are 'right-hand variants', which differ from one or the other of our perfect communicators in just one of the last two digits, applicable only on those rare occasions when an individual is both fed and hurt at the same time. Patterns 00011011 00011010 and 00011011 00011001 differ from a perfect communicator in that they each make just one sound rather than two in the case that they are simultaneously fed and hurt. Patterns 00100111 00100110 and 00100111 00100101 vary from our other perfect communicator in the same way. For our two 'perfect communicators' there are thus also four minimally distinct 'right-hand variants' out of our 65,000 behavioral strategies.

We initially randomize all 28 weights as real values between -3.5 and +3.5 for each of the neural nets in our array. Other details of the model are as before: numbers of food sources and predators, gains and losses, energy costs, the stochastic noise of an imperfect world, and partial training on the highest-scoring neighbor. What differs here is simply the structure of the nets themselves, the full sample space of behavioral strategies, and training by the backpropagation algorithm outlined above.

Full training by backpropagation standardly requires a large number of epochs, each consisting of the complete training set in a randomized order. Here, however, we use only a single training epoch. At the end of each 100 rounds, individuals find any neighbor with a better score and do a partial training on that individual's behavior. Training uses a complete set of possible inputs for each quadrant, in random order, and takes the more successful neighbor's behavioral output for each pair of inputs as target. This cannot, of course, be expected to be a full training in the sense that would make behaviors match; training using a single epoch will typically shift weights only to some degree in a direction that accords with the successful neighbor's behavior. Often the resulting behavior will match neither the initial behavior of the 'trainee' nor the full behavior of its more successful neighbor. In the run outlined below, for example, there are no perfect communicators in the initial randomized array. One version of perfect communicator (00100111 00100111) first appears by partial training in the second century; the other is 'discovered' in the tenth century.

Figure 17 shows a typical result with 1 epoch of training over the course of 300 centuries. Rather than plotting all 65,000 behavioral strategies, we have simplified graphs by showing only those strategies which at one point or another appeared among the top 20 in the array. Here the two strategies that emerge from a sample space of 65,000 are our two 'perfect communicators.' Starting from a randomized configuration it is also possible, however, for one or another 'right- hand variant' to play a significant role as well.

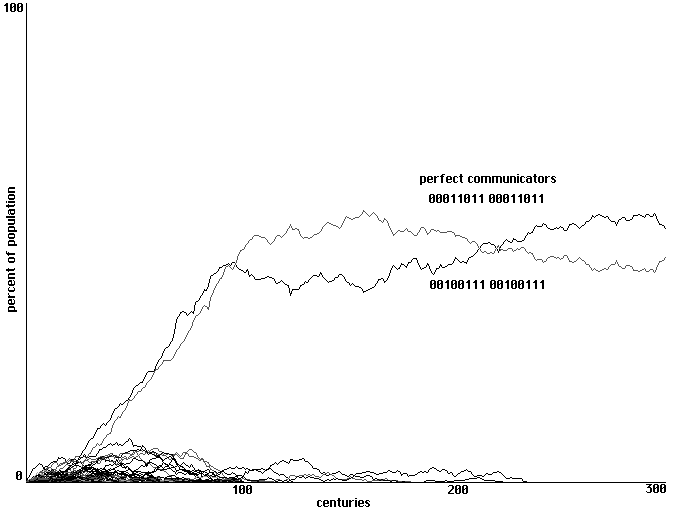
Emergence of perfect communication using backpropagation in an array of randomized neural nets. 1 training epoch used, 300 centuries shown.
Fig. 17
Although one might expect the emergence of perfect communicators to be progressively strengthened by increased numbers of trainings using 2 training epochs, 4, or 8 in place of just 1, for example this turns out not to be the case. Figure 18 shows the result of using 2 training epochs instead of 1 from the same initial randomization. With 2 training epochs our 'perfect communicators' again emerge, this time accompanied by a single 'right-hand variant', but the progression as a whole seems much less steady. Figure 19 shows the result of increasing the number of training epochs to 4. Here neither perfect communicators nor right-hand variants emerge, swamped by the rapid growth of what on analysis seems a very imperfect strategy.

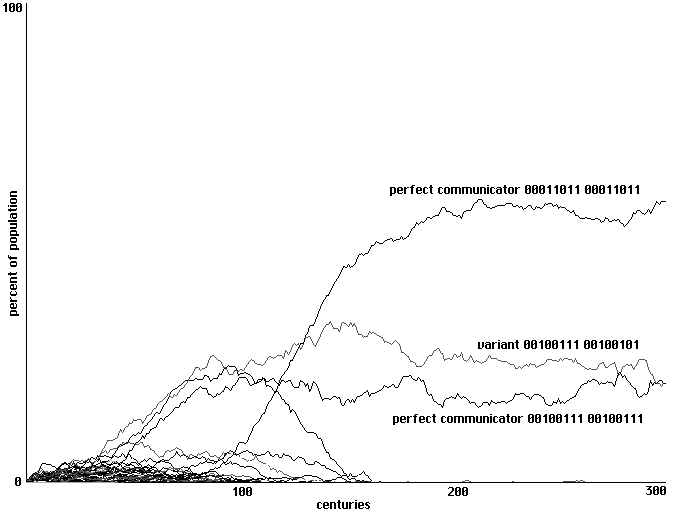
2 training epochs: a rockier development to perfect communication and one right-hand variant. 300 centuries shown.
Fig. 18

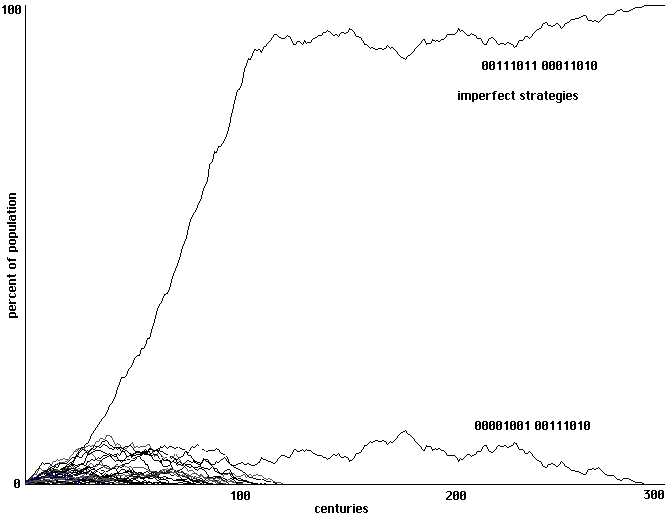
4 training epochs: swamped by quick cloning of imperfect strategies, no perfect communicators or right-hand variants appear. 300 generations shown.
Fig. 19
It is our impression that runs using increasing numbers of training epochs show the negative impact of intensive training. With increasing numbers of training epochs, individuals will more exactly match the behaviors of their successful neighbors; one consequence of that more perfect learning is a less adequate exploration of alternative behavioral strategies, including strategies which might be represented by neither a cell nor its immediate neighbors. In Fig. 19, for example, it appears that intensive training quickly fills the array with clones of a strategy that simply happens to be somewhat more successful than its neighbors early on, despite the fact that it is still a very imperfect communicator. The imperfect learning of merely partial training, in contrast, allows a learning analogue to genetic mutation. With a single training epoch, perfect communicators quickly develop within a randomized array that initially contains none. As Nowak, Plotkin, and Krakauer (1999) note with regard to an otherwise very different model, "language acquisition should be error-prone" (p. 153).

Some further support for such a hypothesis is provided by breaking from the completeness of regimented epochs in order to train less rather than more. In a final variation we train in terms of small numbers of randomized sets of inputs, without any guarantee of covering all input possibilities and indeed without any guarantee against redundancy. Starting from the same initial configuration as before, Figure 20 shows the result of using just two randomized trainings of this sort in place of a training epoch. With just two trainings development is somewhat slower than with the four trainings of a single epoch in Fig. 17, but here again it is our two perfect communicators that clearly emerge.

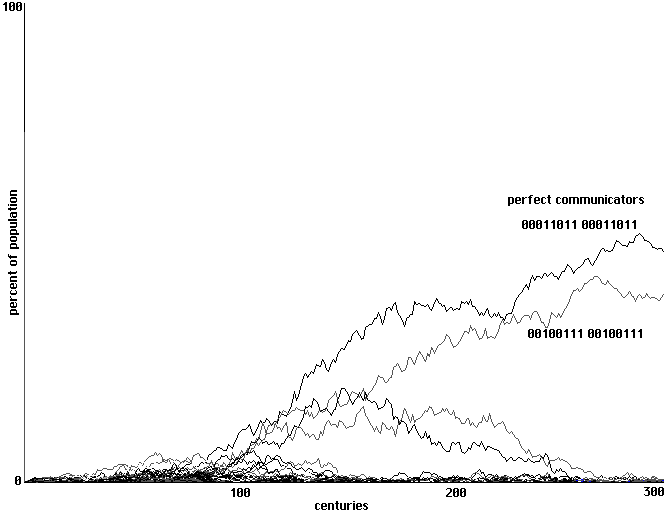
Emergence of perfect communication using backpropagation in an array of randomized neural nets. 2 randomized trainings used, 300 centuries shown.
Fig. 20
The basic pattern we have tracked with simple proto-nets and perceptrons in earlier sections appears here as well, instantiated in the more complete behavioral range of richer neural nets trained using backpropagation. The central lesson is the same throughout: that simple learning routines are sufficient for the emergence of communication in spatialized arrays of randomized neural nets. This holds even when the environment is one in which all gains from communication reflect only individual advantage: where there is no reward for communication per se and indeed where there is a penalty for signaling. In a spatialized environment of wandering food sources and predators, randomized arrays of neural nets learn to communicate.

VI. A Philosophical Conclusion

In previous work we have shown an evolution of communication through mechanisms of imitation (Grim, Kokalis, Tafti, and Kilb, 2000a) and by means of a spatialized genetic algorithm (Grim, Kokalis, Tafti, and Kilb, 2000b). Here our conclusion is that learning algorithms are also adequate for the emergence of communication: that in spatialized arrays of a range of different types of neural nets, simple patterns of signaling emerge and dominate using standard learning algorithms.

In this and earlier studies what we have seen is that (1) basic capabilities for communication--the ability to make and react to arbitrary sounds, for example, together with (2) evolutionary pressure in terms of food gains and predator losses and (3) a mode of strategy change in some sense bootstrapping to the behavior of locally successful neighbors, are together sufficient for the emergence of communities which share a basic signaling system. It does not seem to matter whether strategy change is by pure imitation (Grim, Kokalis, Tafti, and Kilb, 2000a), genetic recombination with code from successful neighbors (Grim, Kokalis, Tafti, and Kilb, 2000b), or the learning algorithms explored here using neural nets. In a spatialized environment, communication emerges with any of these localized modes of strategy change. [9] The emergence of communication isn't picky about its methods.

Genetic algorithms are often conceived as analogues for physical genetics, while the delta rule and backpropagation are thought of as models for learning. If thought of in these terms, the lesson seems to be that simple patterns of communication can emerge either by physical genetics or cultural learning. We are not convinced, however, that the formal mechanism of genetic algorithms need be thought of as applicable solely to physical genetics. Codes in recombination might be taken instead to represent cultural strategies ('memes') that are partially transmitted and combined (Grim, Kokalis, Tafti, and Kilb, 2000b). Nor are we convinced that the learning algorithms typical of neural nets must always be thought of as analogues of cultural learning. In some cases it might be better to view application of the delta rule and backpropagation simply as techniques for strategy change or for exploration of a space of available strategies. Whether accomplished by means of genetic algorithm or backpropagation on neural nets, physical genetics or psychological learning, the emergence of communication might properly be seen as a general process facilitated by the environmental pressures of a spatialized environment.

We suggest that the work above holds a potent philosophical lesson regarding the nature of meaning. In both the tradition of ideational theories of meaning (Aristotle, c. 220 BC; Hobbes, 1651; Locke, 1689; Fodor, 1975), and in much previous modeling work (Levin, 1995; Hutchins and Hazlehurst, 1995; Parisi, 1997; Livingstone and Fyfe, 1999; Nowak, Krakauer and Dress, 1999; Nowak, Plotkin and Krakauer, 1999; Nowak and Krakauer, 1999; Livingstone 2000; Nowak, Plotkin, and Jansen, 2000), the 'meaning' of a sound or gesture is sketched in terms of a correspondence between sound and some internal representation. That picture of meaning is much less plausible here. In the current model, learning proceeds throughout in terms of weight-shifting toward a match to the behavioral strategy of a successful neighbor. When a community of communicators emerges from an array of randomized neural nets, it is convergence to a behavioral strategy that is crucial.

In the model above, there is no guarantee that the internal workings of behaviorally identical strategies in two individuals are themselves identical. There are in principle non- denumerably many neural configurations which may show the same behavioral strategy. In training to match a neighboring 'perfect communicator', a neural net may not only fail to match the absolute values of its neighbor's weights, but may not even match its over-all structure of relative weight balances. What arises in a community is a pattern of coordinated behavior, but in evolving from an initially randomized array of neural nets that coordinated behavior need not be built on any uniform understructure in the nets themselves. There is thus no guarantee of matching internal representations in any clear sense, no guarantee of matching internal 'meanings', and no need for internal matches in the origin and maintenance of patterns of communication across a community.

The basic philosophical lesson is a Wittgensteinian one, here given a more formal instantiation and a richer evolutionary background. 'Meaning' in the present model is essentially a coordination of cooperative behavior in terms of sounds or gestures produced and received. We take this to be an indication of the right way to approach meaning both philosophically and model-theoretically. 'Meanings' are not to be taken to be things, either objective things in the world or subjective things in individual heads. Nor is meaning to be read off in terms of some internal 'mentalese' (Fodor, 1975). Meaning is less individual and less internal than that, more cooperative and more historical. To understand meaning is to understand the historical coordination of a particular type of cooperative behavior. Although we are no fans of his carefully crafted obscurity, we think this is in accord with the general Wittgensteinian lesson that "...to imagine a language means to imagine a way of life" (1953, 19).

Notes

For a more complete outline of rival philosophical approaches see Ludlow (1997). [back]
It is also possible, of course, that different aspects of meaning may call for different approaches. There are clearly compositional aspects of full-fledged languages, for example, that a model as simple as ours will not be able to capture. [back]
In this simple model, in fact, neither weights nor outputs can equal zero. [back]
The reason for using twice as many predators as food items is detailed in Grim, Kokalis, Tafti, and Kilb (2000b). A bit of reflection on the dynamics of feeding and predation built into the model shows an important and perhaps surprising difference between the two. In an array composed entirely of 'communicators', a chain reaction can be expected in terms of food signals and successful feeding. One communicator signals that it has been fed, with the result that its neighbors open their mouths on the next round. The wandering food item then lands on one of neighbors (or the original cell), and that cell in turn makes a sound which signals its neighbors to open their mouths. As illustrated in Fig. 2, one can watch a wandering food item cross an array of communicators, hitting an open mouth every time. The dynamics of a 'hurt' alarm, on the other hand, are very different. Among even perfect communicators, a cell signals an alarm only when hurt--that is, when a predator is on it and it is not hiding. If successful, that 'alarm' will alert a cell's neighbors to hide, and thus the predator will find no victim on the next round. Precisely because the predator then finds no victim, there will be no alarm sounded, and thus on the following round even a fellow 'communicator' may be hit by the predator. Here one sees not the chain reaction of successful feeding on every round but an alternating pattern of successful avoidance of predation every second round. An important difference between the dynamics of feeding and predation is thus built into the structure of the model. With a gain for feeding equal to a loss for predation, and with equal numbers of food sources and predators, that difference in dynamics means that emergence of communication regarding food will be strongly favored over communication regarding predators by the structure of the model. This is indeed what we found in earlier genetic models (Grim, Kokalis, Tafti, and Kilb, 2000b). One way of compensating for the difference in order to study emergence of communication regarding both food and predators is to build in losses from predation which are unequal to gains from feeding. Another is to have an alarm signal which indicates the presence of a predator whether or not one is 'hurt'. A third alternative, which we have chosen here, is simply to proportion food sources and predators accordingly. [back]
Where an initial randomization does happen to contain a single cell for a perfect communicator, moreover, that strategy is often extinguished in the second or third generation; a lone perfect communicator is not guaranteed any particular advantage, and in many situations suffers a significant disadvantage because of energy costs. In such arrays perfect communication re-emerges at a later point by partial training. [back]
It is also possible for one of our two perfect communicators to predominate simply because it appears first and quickly occupies territory. [back]
We are deeply indebted to Laurene Fausett for helpful correspondence regarding training algorithms for nets of the structure used here. Our simple net combines perceptron-like connections (along weights w1 and w4) with crucial use of a single hidden node; it will be noted that the training algorithm also combines a perceptron-like training for w1, w4, and w5 with full backpropagation to update w2 and w3. [back]
Those Booleans to which training was not possible were in all cases exclusive 'or' or the biconditional. We also explored non-standard forms of backpropagation which did prove adequate for training 100% of our initial weight sets to each of the 16 Booleans. Final results were very similar to those outlined. [back]
Although we have some hypotheses, we can't yet claim to know precisely what it is about spatialization that favors either cooperation (Grim 1995, 1996) or the triumph of communicators over parasitic variants here and in earlier studies (Grim, Kokalis, Tafti, and Kilb, 2000a; Grim, Kokalis, Tafti, and Kilb, 2000b). A more analytic treatment of spatialization remains for further work. [back]

Acknowledgements

We are obliged to Nicholas Kilb and Ali Tafti for important discussion in the early stages of the project, to Laurene Fausett for gracious counsel on technical points, and to Evan Conyers and two anonymous referees for detailed and helpful comments.

back to Patrick Grim's page