Figure 1. Time series graph.
"The strategies for making mathematical models for observed phenomena have been evolving since ancient times. An organism-- physical, biological, or social-- is observed in different states. This observed system is the target of the modeling activity. Its states cannot really be described by only a few observable parameters, but we pretend that they can."
--Ralph Abraham and Christopher Shaw, Dynamics: The Geometry of Behavior1
"Computers are useless. They can only give you answers."
--Pablo Picasso2
This book is an introduction, entirely by example, to the possibilities of using computer models as tools in philosophical research in general and in philosophical logic in particular. The accompanying software contains a variety of working examples, in color and often operating dynamically, embedded in a text which parallels that of the book. In order to facilitate further experimentation and further research, we have also included all basic source code in the software.
A picture is worth a thousand words, and what computer modeling might mean in philosophical research is best illustrated by example. We begin with an intuitive introduction to three very simple models. More sophisticated versions and richer variatons are presented with greater philosophical care in the chapters that follow.
"I made a practice of wandering about the common every night from eleven till one, by which means I came to know the three different noises made by nightjars. (Most people only know one.) I was trying hard to solve the contradictions [of the set-theoretical paradoxes]. Every morning I would sit down before a blank sheet of paper. Throughout the day, with a brief interval for lunch, I would stare at the blank sheet. Often when evening came it was still empty... It was clear to me that I could not get on without solving the contradictions, and I was determined that no difficulty should turn me aside from the completion of Principia Mathematica, but it seemed quite likely that the whole of the rest of my life might be consumed in looking at that blank sheet of paper. What made it the more annoying was that the contradictions were trivial, and that my time was spent in considering matters that seemed unworthy of serious attention."
--Bertrand Russell, Autobiography: The Early Years3
Consider the Liar Paradox:
| The boxed sentence is
false. |
Is that sentence true, or is it false?
Let's start by supposing it is true. What it says is that it is false. So if we start by assuming it true it appears we're forced to change our verdict: it must be false.
Our verdict now, then, is that the boxed sentence is false. But here again we run into the fact that what the sentence says is that it is false. If what it says is that it is false and it is false, it appears it must be true.
We're back again to supposing that the boxed sentence is true.
This kind of informal thinking about the Liar exhibits a clear and simple dynamics: a supposition of true' forces us to ‘false', the supposition of ‘false' forces us back to ‘true', the supposition of ‘true' forces us back to ‘false', and so forth. We can get a very simple model for that intuitive dynamics in terms of a graph.
As in figure 1, we will let 1 represent ‘true' at the top of our graph, and let 0 represent ‘false' at the bottom. The stages of our intuitive deliberation-- ‘now it looks like it's true...but now it looks like it's false...' --will be marked as if in moments of time proceeding from left to right.

Figure 1. Time series graph.
This kind of graph is known as a time-series graph. In this first simple philosophical application, a time-series graph allows us to map the dynamic behavior of our intuitive reasoning for the Liar as in figure 2.4
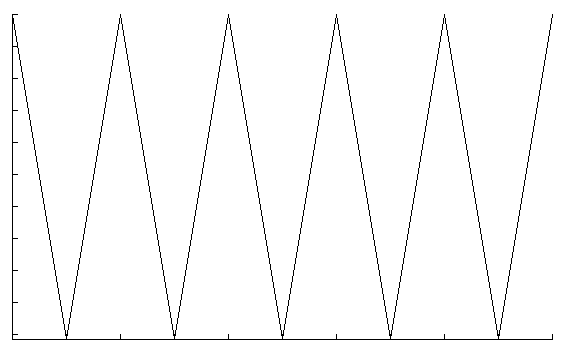
Figure 2. Time series graph for intuitive reasoning of the Liar. (A Java applet that draws the above image...)
This simple model is the basic foundation of some of the work of chapter 1, though of course only the foundation. There such a model is both carried into infinite-valued or fuzzy logics and applied to wide range of self-referential sentences. One of these-- the Chaotic Liar-- has the dynamics portrayed in figure 3.

Figure 3. Time series graph for the Chaotic Liar. (A Java applet that draws the above image...)
The model itself suggests richer elaborations, offering images for mutually referential sentences such as that shown in figure 4. Similar modeling is extended to some intriguing kinds of epistemic instability in chapter 2.

Figure 4. Escape-time diagram for a Dualist form of the Liar.
The logician Jan Lukasiewicz speaks of his deepest intuitive feelings for logic in terms of a picture of an independent and unchangeable logical object:
"...I should like to sketch a picture connected with the deepest intuitive feelings I always get about logistic. This picture perhaps throws more light than any discursive exposition would on the real foundations from which this science grows (at least so far as I am concerned). Whenever I am occupied even with the tiniest logistical problem, e.g. trying to find the shortest axiom of the implicational calculus, I have the impression that I am confronted with a mighty construction, of indescribable complexity and immeasurable rigidity. This construction has the effect upon me of a concrete tangible object, fashioned from the hardest of materials, a hundred times stronger than concrete and steel. I cannot change anything in it; by intense labour I merely find in it ever new details, and attain unshakeable and eternal truths."
--Jan Lukasiewicz, W obronie Logistyki5
Here we offer another simple model, one we develope further in chapter 3 in the attempt to capture something like a Lukasiewiczian picture of formal systems as a whole.
As any beginning student of formal logic knows, a sentence letter p is thought of as having two possible values, true or false:
| p |
|---|
| T |
| F |
It is in terms of these that we draw a simple truth-table showing corresponding values for ‘not p': if p happens to be true, ‘not p' must be false; if p happens to be false, ‘not p' must be true:
| p | ~p |
|---|---|
| T | F |
| F | T |
What we've drawn for p and ~p are two two-line truth tables. But these are of course not the only two-line combinations possible. We get all four possibilities if we add combinations for tautologies, thought of as always true, and contradictions, thought of as always false:
 | p | ~p |
 |
|---|---|---|---|
| F | T | F | T |
| F | F | T | T |
Now consider the possibility of assigning each of these combinations of truth and falsity a different color:
 |  |  |  |
 | p | ~p |
 |
|---|---|---|---|
| F | T | F | T |
| F | F | T | T |
With these colors for basic value combinations we can paint simple portraits of classical connectives such as conjunction (‘and') and disjunction (‘or'). Figure 5 is a portrait of conjunction: the value colors on its axes combine in conjunction to give the values at points of intersection. The conjunction of black with black in the upper left corner, for example, gives us black, indicating that the conjunction of two contradictions is a contradiction as well.

Figure 5. Value matrix for conjunction.
Figure 6 is a similar portrait of disjunction. When we put the two images side by side it becomes obvious that they have a certain symmetry: the symmetry standardly captured by speaking of disjunction and conjunction as dual operators.6

Figure 6. Value matrix for disjunction.
What this offers is a very simple matrix model for logical operators. In chapter 3 we attempt to extend the model so as to depict formal systems as a whole, allowing us also to highlight some surprising formal relationships between quite different formal systems. One result is the appearance of classical fractal patterns within value portraits much like that outlined above. Figure 7 shows the pattern of tautologies in a more complicated value space, here for the operator NAND (or the Sheffer stroke) and for a system with 3 sentence letters and thus 256 possible truth-table columns. The image that appears is familiar within fractal geometry as the Sierpinski gasket.7

Figure 7. Tautologies in a value space for 3 sentence letters: the Sierpinski gasket.
Imagine a group of people beyond the powers of any government, all of whom are out for themselves alone: an anarchistic society of self-serving egoists. This is what Hobbes imagines as a state of war, "where every man is Enemy to every man," and in which the life of man, as a result, is "solitary, poore, nasty, brutish, and short".8
How might social cooperation emerge in a society of egoists? This is Hobbes's central question, and one he answers in terms of two ‘general rules of Reason'. Since there can be no security in a state of war, it will be clear to all rational agents "that every man, ought to endeavor peace, as farre as he has hope of obtaining it; and when he cannot obtain it, that he may seek, and use, all helps and advantages of Warre". From this Hobbes claims to derive a second rational principle: "That a man be willing, when others are so too...to lay down this right to all things; and be contented with so much liberty against other men, as he would allow other men against himselfe."9
In later chapters we develop some very Hobbesian models of social interaction using game theory within cellular automata (akin to the ‘Game of Life').10 The basic question is the same: How might social cooperation emerge within a society of self-serving egoists? Interestingly, the model-theoretic answers that seem to emerge often echo Hobbes's second principle.
The most studied model of social interaction in game theory is undoubtedly the Prisoner's Dilemma. Here we envisage two players who must simultaneously make a ‘move', choosing either to ‘cooperate' with the other player or to ‘defect' against the other player. What the standard Prisoner's Dilemma matrix dictates is how much each player will gain or lose on a given move, depending on the mutual pattern of cooperation and defection:
| Player A | |||
|---|---|---|---|
| C | D | ||
| Player B | C | (3,3) | (0,5) |
| D | (5,0) | (1,1) | |
If both players cooperate on a single move, both get 3 points. If both defect, each gets only 1 point. But if one player defects and the other cooperates, the defector gets a full 5 points and the cooperator walks away with nothing. Because it favors both mutual cooperation and individual defection, the Prisoner's Dilemma has been widely used to study options for cooperation in an egoistic society. In a model that we use extensively in later chapters, members of a society are envisaged in a spatial array, following particular strategies in repeated Prisoner's Dilemma exchanges with their neighbors. Figure 8, for example, shows a randomized array in which each cell represents a single individual and each color represents one of eight simple strategies for repeated play.

Figure 8. Randomized spacial array of eight prisoner's dilemma strategies.
Some of these are vicious strategies, in the sense of always defecting against their neighbors. Some are extremely generous, in the sense of cooperating no matter how often they are burned. A strategy of particular interest, called ‘Tit for Tat', returns like for like, cooperating with a cooperative partner but defecting against a defector. ‘Tit for Tat' carries a clear echo of Hobbes' second ‘rule of Reason': "Whatsoever you require that others should do to you, that do ye to them".11
Some strategies, in some environments, will be more successful than others in accumulating Prisoner's Dilemma points in games with their neighbors. How will a society evolve if we have cells convert to the strategy of their most successful neighbor? Will defection dominate, for example, or will generosity?
Figure 9 shows a typical evolution in a very simple case, in which Tit for Tat evolves as the standard strategy.
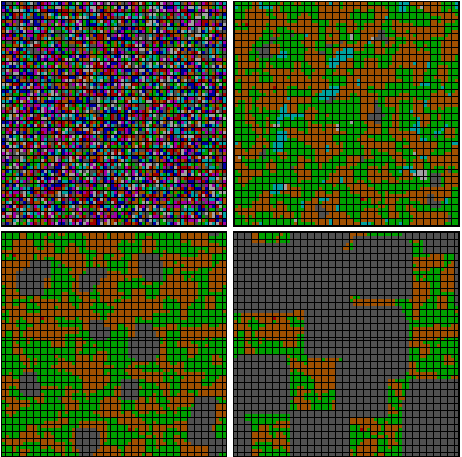
Figure 9. Evolution of randomized array toward dominance by Tit for Tat. (Click to see a Java applet that draws the above image. Because the display is randomized each time, repeats will give different evolutions.)
In later chapters we explore more complicated variations on such a model, using ranges of more complicated meta-strategies and introducing forms of cooperation and defection ‘imperfect' both probabilistically and in terms of degrees. An undecidability result for even a very simple spatialized Prisoner's Dilemma appears in chapter 6.
Here we've started with three simple examples of philosophical modeling--simple so as to start simple, but also representative of some basic kinds of models used in the real work of later chapters.
We are in fact heirs to a long tradition of philosophical modeling, extending from Plato's Cave and the Divided Line to models of social contracts and Rawls' original position. If one is looking for philosophical models, one can find them in Heraclitus's river, in Plato's charioteer model of the tripartite soul, in Aristotle's squares of opposition, in Dante's levels of the Inferno, Purgatorio, and Paradiso, in Locke's impressions on the mind and Descartes' captained soul in the sixth meditation. Logic as a whole, in fact, can be looked upon as a tradition of attempts to model patterns of inference. Philosophical modeling is nothing new.
In many cases, philosophical models might be thought of as thought experiments with a particularly vivid and sometimes intricate structure. Just as thought experiments are more than expository devices, so models can be. The attempt to build intellectual models can itself enforce requirements of clarity and explicitness, and can make implications clear that might not be clear without an attempt at explicit modeling. The making of models can also suggest new hypotheses or new lines of approach, showing when an approach is unexpectedly fruitful or when it faces unexpected difficulties.
The examples of computer modeling we introduce here are conceived of in precisely this tradition of philosophical model-building and thought experiments. All that is new are the astounding computational resources now available for philosophical modeling.
As our subtitle indicates, we conceive of the chapters that follow as explorations in philosophical computer modeling. In no case are they intended as the final word on the topics addressed; we hope rather that they offer some suggestive first words that may stimulate others to carry the research further. The topics addressed in the following essays, moreover-- paradoxes and fuzzy logic, fractals and simple formal systems, egoism and altruism in game theory and cellular automata-- are merely those topics to which our curiosities have happened to lead us. We don't intend them in any sense as a survey of ways in which computer modeling might be used; indeed our hope is that these exploratory essays will stimulate others to explorations of quite different philosophical questions as well.
In each of the following chapters the computer allows us to literally see things the complexity of which would otherwise be beyond our computational reach: fractal images showing the semantic behavior of a wide range of pairs of mutually referential sentences, vivid images of patterns of contradiction and tautology in formal systems, and evolving visual arrays demonstrating a wide social effect of local game-theoretic interactions. Whether these answer questions which we might not have been able to answer without them is another matter. Often our logical results, such as the formal indefinability of chaos in chapter 1 or the undecidability of the Spatialized Prisoner's Dilemma in chapter 6, were suggested by our computer work but might also conceivably have been proven without it. We don't want to claim, then--at least not yet-- that the computer is answering philosophical questions that would be in principle unanswerable without it. In no way do the astounding computational abilities of contemporary machines offer a substitute for philosophical research. But we do think that they offer an important new environment for philosophical research.
Our experience is that the environment of computer modeling often leads one to ask new questions, or to ask old questions in new ways-- questions about chaos within patterns of paradoxical reasoning or epistemic crises, for example, or Hobbesian questions asked within a spatialization of game-theoretic strategies. Such an environment also enforces, unflinchingly and without compromise, the central philosophical desideratum of clarity: one is forced to construct theory in the form of fully explicit models, so detailed and complete that they can be programmed. With the astounding computational resources of contemporary machines, moreover, hidden and unexpected consequences of simple theories can become glaringly obvious: "A computer will do what you tell it to do, but that may be much different from what you had in mind."12
Although difficult to characterize, it is also clear from experience that computer modeling offers a possibility for thoroughly conceptual work that is nonetheless undeniably experimental in character. Simple theories can be tested in a range of modeled counterfactual ‘possible worlds'-- Hobbesian models can be tested in worlds with and without perfect information or communication, for example, or with a greater or lesser Rawlsian ‘veil of ignorance'. One can also, however, test theoretical variations essentially at will, feeling one's way through experimental manipulation toward a conceptual core: an hypothesis of precisely what it is about a theory that accounts for the appearance of certain results in certain possible worlds.
It must also be admitted with regard to computer modeling-- as with regard to philosophical or intellectual modeling in general-- that models can fail. All models are built with major limitations-- indeed that is the very purpose of models. Models prove useful both in exposition and exploration precisely because they're simpler, and therefore easier to handle and easier to track, than the bewildering richness of the full phenomena under study. But the possibility always remains that one's model captures too few aspects of the full phenomenon, or that it captures accidental rather than essential features. One purpose of labeling ours as explorations in computer modeling is to emphasize that they may fail in this way. When and where they fall short, however, it will be better models that we will have to strive for.
Computer modeling is new in philosophy and thus maybe misunderstood. We should therefore make it clear from the beginning what the book is not about. What is at issue here is not merely the use of computers for teaching logic or philosophy. That has its place, and indeed the Logic Lab in which much of this work emerged was established as a computer lab for teaching logic. Here, however, our concentration is entirely on exploratory examples of the use of computer modeling in philosophical research. We will also have little to say that will qualify as philosophy of computation or philosophy about computers-- philosophical discussions of the prospects for modeling intelligence or consciousness, for example, or about how computer technology may affect society. Those too are worthy topics, but they aren't our topic here. Our concern is solely with philosophical research in the context of computer modeling.
Our ultimate hope is that others will find an environment of computer modeling as philosophically promising as we have. We offer a handful of sample explorations with operating software and accessible source code in the hope that some of our readers will not only enjoy some of these initial explorations but will find tools useful in carrying the exploration further.
We attempt throughout to make our explanations of the modeling elements we use as simple and self-contained as possible. Some readers, however, may wish more background on the elements themselves. For each of the topics below we've tried to suggest an easy popular introduction-- the first book listed-- as well as a more advanced but still accessible text.
Cellular Automata
1. Redwood City, California: Addison-Wesley, 1992; p. 15
2. Quoted in Clifford A. Pickover, Computers, Pattern, Chaos and Beauty, New York: St. Martin's Press, 1990, p. 10.
3. Autobiography, vol. 1, New York: Bantam Books, 1951, pp. 200-201.
4. Here it is of course only the alternation between True and False at discrete points of deliberation that is graphed. ‘Bounce' lines between points of deliberation are not meant to indicate that deliberation passes through intermediate truth values.
5. In Z zaganien logiki i filozofii, Warsaw: Paustwowe Wydawnictwo Naukowe, 1961, tr. by Peter Geach in A Wittgenstein Workbook, Berkeley: University of California Press, 1970, p. 22.
6. See for example W. V. Quine, Methods of Logic, New York: Holt, Rinehart, and Winston, 1959.
7. See for example Manfred Schroeder, Fractals, Chaos, Power Laws, New York: W. H. Freeman and company, 1991.
8. Hobbes, Leviathan, Part I, ch. 13.
9. Hobbes, Leviathan, Part I, ch. 14.
10. John Horton Conway's ‘Game of Life' itself plays an important role in a later chapter on ‘Real Life' and in the background motivation for the undecidability result of chapter seven. Hobbes himself, interestingly enough, begins the Leviathan by asking "may not we say, that all Automata have ... an artificiall life?"
11. Hobbes, Leviathan, Part I, ch. 14.
12. Joseph Weizenbaum, quoted in Time, The Merriam-Webster Dictionary of Quotations, 1996.