
Evolution of Communication with a Spatialized Genetic Algorithm
Patrick Grim, Trina Kokalis, Ali Tafti, and Nicholas Kilb
Evolution of Communication 3 (2001), 105-134
Group for Logic & Formal Semantics
Dept. of Philosophy, SUNY at Stony Brook
Abstract:
We extend previous work by modeling evolution of communication using a spatialized genetic algorithm which recombines strategies purely locally. Here cellular automata are used as a spatialized environment in which individuals gain points by capturing drifting food items and are 'harmed' if they fail to hide from migrating predators. Our individuals are capable of making one of two arbitrary sounds, heard only locally by their immediate neighbors. They can respond to sounds from their neighbors by opening their mouths or by hiding. By opening their mouths in the presence of food they maximize gains; by hiding when a predator is present they minimize losses. We consider the result a 'natural' template for benefits from communication; unlike a range of other studies, it is here only the recipient of communicated information that immediately benefits.
A community of 'perfect communicators' could be expected to make a particular sound when successfully feeding, responding to that same sound from their neighbors by opening their mouths. They could be expected to make a different sound when 'hurt' and respond to that second sound from their neighbors by hiding.
Suppose one starts from a small set of 'Adam and Eve' strategies randomized across a cellular automata array, and uses a genetic algorithm which operates purely locally by cross-breeding strategies with their most successful neighbors. Can one, in such an environment, expect evolution of local communities of 'perfect communicators'? With some important qualifications, the answer is 'yes'.
Keywords: communication, evolution, spatialization, genetic algorithm, philosophy of language.
1. Introduction
Although philosophers have long been interested in meaning, we think they have been hampered by the limits of the conceptual tools at their disposal. In the most common approach, philosophers have tried to understand meaning in terms of linguistic intuitions revealed in the introspection of individual language users. In a more formal vein they have sometimes tried to model meaning on aspects of axiomatic systems borrowed from mathematical logic. In a third approach, philosophers have appealed to simplified social models such as the 'slab' games of Wittgenstein's Brown Book.
Our strongest affinities are with this third philosophical approach, involving simplified social models. We share with that approach the conviction that meaning will most profitably be understood 'from the outside', not as a mental phenomenon internal to individuals but as a phenomenon of behavioral coordination across a community. Our attempt here, however, is to develop such a tradition with the more sophisticated tools of computer modeling.
The model we offer for simple patterns of communication is one in which development over time is essential: our guess is that the genesis of linguistic meaning will be best understood in terms of a historically evolving coordination of behavioral repertoires. Ours is therefore a model in which meaning appears as a behavioral property rather than a mentally introspectible one, as a property best understood in its development over time rather than at any single time slice, and as a property essentially of a community rather than an individual.(1)
Despite the complications of our philosophical motivations, the model we have to offer is a simple one. In Grim, Kokalis, Tafti, and Kilb 1999 we considered cellular automata arrays of individual cells which gain points by 'feeding' and lose points by 'failing to feed' on a swarm of migrating food sources that move past them.(2) Each cell in that earlier work was capable of making a single sound heard by its immediate neighbors, was capable of hearing sounds made by its neighbors, and bore a simple behavioral strategy that dictated its response to sound, to silence, and to feeding or failing to feed. An individual's strategy specified when it would make the sound at its disposal and how it would react to hearing a sound from its immediate neighbors.
In that study we carefully limited ourselves to the simplest possible strategies. We also used a simple pattern of strategy change: after a series of runs, individual cells would compare their total score with that of their neighbors and would adopt the strategy of any neighbor that proved more successful. Even in that simple model, elementary forms of signaling could be seen to evolve. Stochastic forms of communicative strategies, in particular-strategies which both responded to food by making a certain sound, which we labeled S1, and responded to that sound S1 by mouth-opening, for example-proved evolutionarily advantageous.(3) Communities of these 'communicators' spread progressively across the spatial array.
That earlier structure allowed us to explore only a small sample space of strategies, however, and mechanisms of strategy change were limited to those strategies originally represented within the array. Here we offer a series of more developed models. All models continue the tradition of local action: our individuals are still sensitive only to events in their immediate neighborhood. Here we outline a richer environment, however, in which there are both potential gains from capturing 'food' and potential losses from being hit by a 'predator'. The sample space of strategies is far larger. Our individuals are capable, moreover, of making and responding to either of two arbitrary sounds or to silence. In the more advanced models of this series they also have a wider behavioral repertoire: they can open their mouths (appropriate in the presence of food), hide (appropriate in order to avoid predators), or 'rest' in a third neutral state. Hiding and mouth-opening carry a tax for energy expended that the neutral state avoids.
The most important difference between this and our earlier work, however, is the mode of strategy change employed. There cells merely copied the strategy of successful neighbors. Here they 'breed' new strategies, using a genetic algorithm to produce new strategies in combination with those of their most successful neighbor. Strategies thus arise from mechanisms of combination which do not exist at earlier stages in the evolution of an array. Unlike a range of other studies, recombination by genetic algorithm is here applied purely locally, generating recombinations from particular cells and their most successful neighbors, rather than globally across the population as a whole. We consider it a 'natural' feature of this model that reproduction, like feeding, predation, and sound communication, proceeds purely locally. Spatialized reproduction may also alleviate some of the perennial problems of genetic algorithms, more effectively avoiding premature convergence and local maxima by better maintaining genetic variety.
With recombination by local genetic algorithm we no longer need to start with an initial randomization that represents all possible strategies; we can start instead with a mere handful of 'Adams and Eves'. None of these will prove to be the most successful strategy in the end, but from them a wide range of hybrid strategies will develop. Here as in our earlier work we can expect successful strategies to occupy progressively more territory within an array, but in the present study it is purely through the mechanism of localized genetic algorithm that strategies will arise and spread. What we want to know, in a model with this richer environment and this spatialized mechanism for a wider sampling of more complicated strategies, is whether simple patterns of behavioral coordination with the hallmarks of signaling or communication will evolve.
For purposes of further research all essential software is available from the authors on request.
2. Other Genetic Algorithms for Communication
There are few previous models for communication of the sort we outline here. MacLennan 1991 proposes a model in which 'senders' and 'receivers' are both rewarded in cases of successful communication involving arbitrary symbols, and in which communicative strategies are perfected through the application of a genetic algorithm. A major limitation of MacLennan's model is that communication does not arise as a consequence of 'natural' benefits to the receiver alone. Instead, communicative matches are judged for success by some external observer, as it were, and both parties are rewarded when a match is made. As Ackley and Littman 1994 note, the result is an artificial environment "where 'truthful speech' by a speaker and 'right action' by a listener causes food to rain down on both." Selection which rewards mutual understanding per se, rather than tracking individualized benefit gained from information communicated, reappears in Levin 1995.(4) Rewards for senders and receivers are again mutual in MacLennan and Burghardt 1994 and Wagner forthcoming, but in these studies there is at least a more developed motivation: both studies are explicitly limited to communication regarding cooperative activities in particular, in which for example several individuals are required to bring down a large animal. For that reason they cannot generalize to communication in general, however.
The need for answers as to how communication can arise in the general case, where it is of immediate benefit only to the receiver, is explicitly called for in Ackley and Littman 1994, Cangelosi and Parisi 1998, and Batali unpublished. That more natural pattern of benefits is one essential characteristic of the model developed here.
Werner and Dyer 1991 introduce a feature that the current model shares: a spatialized population. Their model is limited to communication which facilitates reproduction by allowing 'males' and 'females' to find each other more rapidly, however, and the fact that new strategies are generated from global mixing rather than local reproduction seems to limit the lessons that might be learned from spatialization.(5) Some aspects of environmental spatialization, although limited to communication regarding cooperative activities, also appear in MacLennan and Burghardt 1994 and Wagner forthcoming. But here again reproduction fails to be included in the spatialization: recombination proceeds always in terms of a global genetic algorithm which mates individuals with the highest 'fitness' across an entire population.
In the present study, in contrast, we have spatialized everything. Individuals gain and lose points by capturing food and avoiding predators at their own particular location, and sounds made by individuals can be heard only within a certain range. Strategy change proceeds by genetic algorithm, but here all reproduction is local as well: individuals breed purely locally with their most successful neighbors.(6)
The previous model that is closest to ours is perhaps Ackley and Littman 1994, which attempts to improve on earlier attempts by studying the evolution of communication in at least a limited spatial environment and with a more natural distribution of rewards for gaining food and avoiding predators. Unlike studies noted above, theirs is one which rewards communication only indirectly as it contributes to an individual's successful feeding and avoidance of harm. Theirs is also a model in which a genetic algorithm is applied with some locality, breeding those individuals in a 'quad' with the highest fitness ratings.
Ackley and Littman immediately complicate their model, however, with a blizzard of further interacting factors: a hierarchy of different organizational levels with different patterns for scoring and change on different levels, a distinction throughout between genotype and phenotype, the complications of 32-unit neural nets coded with both synaptic specification genes and pseudo-genes which are then processed by genetic algorithm, and last but not least reproductive 'festivals' declared at official holidays and a peculiar wind-driven strategy diffusion. We consider Ackley and Littman's work to be a warning against over-ambitious and baroque model building: their conclusions prove difficult to interpret precisely because the model is itself so unnecessarily complicated.
In terms of general approach, rather than modeling details, we consider the closest philosophical ancestor of our work to be that of Skyrms 1996, itself a sophisticated response to the groundbreaking study of convention and coordination problems in Lewis 1969.
3. Parameters of the Model: Before the Genetic Algorithm
We begin by outlining some of the basic parameters of the modeling environment. The recombinant mechanism of genetic algorithms will then be introduced as a further development.
We use a randomized 64 x 64 two-dimensional cellular automata array of 'individuals' carrying different strategies. Technically, the array forms a torus, 'wrapping around' so that individuals on the bottom edge have neighbors at the top edge, those at the left edge have neighbors on the right, etc. The individual cells themselves are thought of as stationary, perhaps like coral in a reef. There are also food sources that migrate in a random walk through the array, and predators that wander in the same fashion. Total numbers of food sources and predators may be adjusted in different runs, though the number of each is here kept constant through the course of any given run.
In a given run we might work with 50 food sources and 50 predators. If a food source lands on a cell with its mouth open, that individual 'eats' and thus gains points. The food source does not then disappear, however, which is one reason we think of these as food sources rather than individual items of consumption. If a predator lands on a cell that is not 'hiding', that individual is 'harmed' and loses points. The positive gains for 'eating' and losses for 'harming' can be adjusted in experiment as well.
Our individual cells are capable of making one of two sounds on a given round, which we term S1 and S2. An individual's sounds are heard only by his eight immediate neighbors. Each cell carries a strategy that dictates its behavior-hiding or opening its mouth, for example- depending on whether the cell has just heard a particular sound.
In background tests before the introduction of a genetic algorithm, we envisaged each cell as either opening its mouth or hiding on each round. Our strategies were four-tuples <f, h, s1, s2>, with three possibilities for each variable: such a strategy specifies what the individual does when fed f (make no sound, make sound S1, or make sound S2), what it does when hurt h (the same three options), what it does when it hears a sound S1 (eat, hide, or a random selection between the two), and what it does when it hears a sound S2 (the same options). When no sound is heard, a random flip of a coin dictates whether a cell will open its mouth or hide.(7)
This first model is therefore structured in terms of 81 strategies. These can be envisaged in base 3 as follow:
<0,0,0,0> never sounds and continues to behave randomly (hiding or opening its mouth) on hearing any sound.
<0,0,0,1> never sounds, behaves randomly on hearing S1, but opens its mouth on hearing S2
<0,0,0,2> never sounds, behaves randomly on hearing S1, but hides on hearing S2
<0,0,1,0> never sounds, opens its mouth on hearing S1, behaves randomly on hearing S2
<0,0,1,1> never sounds, opens its mouth on hearing either S1 or S2
<0,0,1,2> never sounds, opens its mouth on hearing S1and hides on hearing S2
<0,0,2,0> never sounds, hides on hearing S1 and behaves randomly on hearing S2
<0,0,2,1> never sounds, hides on hearing S1 but opens its mouth on hearing S2
<0,0,2,2> never sounds, hides on hearing any sound
<0,1,0,0> sounds S1 when hurt, behaves randomly on hearing any sound.
<0,1,0,1> sounds S1 when hurt, behaves randomly on hearing S1, but opens its mouth on hearing S2
<0,1,0,2> sounds S1 when hurt, behaves randomly on hearing S1, but hides on hearing S2
<0,1,1,0> sounds S1 when hurt, opens its mouth on hearing S1, behaves randomly on hearing S2
<0,1,1,1> sounds S1 when hurt, opens its mouth on hearing either S1 or S2
<0,1,1,2> sounds S1 when hurt, opens its mouth on hearing S1 and hides on hearing S2
<0,1,2,0> sounds S1 when hurt, hides on hearing S1 and behaves randomly on hearing S2
<0,1,2,1> sounds S1 when hurt, hides on hearing S1 but eats on hearing S2
<0,1,2,2> sounds S1 when hurt, hides on hearing any sound
<0,2,0,0> sounds S2 when hurt, behaves randomly on hearing any sound.
<0,2,0,0> sounds S2 when hurt, behaves randomly on hearing any sound.
<0,2,0,1> sounds S2 when hurt, behaves randomly on hearing S1, but opens its mouth on hearing S2
<0,2,0,2> sounds S2 when hurt, behaves randomly on hearing S1, but hides on hearing S2
<0,2,1,0> sounds S2 when hurt, opens its mouth on hearing S1, behaves randomly on hearing S2
<0,2,1,1> sounds S2 when hurt, opens its mouth on hearing either S1 or S2
<0,2,1,2> sounds S2 when hurt, opens its mouth on hearing S1 and hides on hearing S2
<0,2,2,0> sounds S2 when hurt, hides on hearing S1 and behaves randomly on hearing S2
<0,2,2,1> sounds S2 when hurt, hides on hearing S1 but eats on hearing S2
<0,2,2,2> sounds S2 when hurt, hides on hearing any sound
<1,0,0,0> sounds S1 when fed, behaves randomly on hearing any sound
<1,0,0,1> sounds S1 when fed, behaves randomly on hearing S1, opens its mouth on hearing S2
<1,0,0,2> sounds S1 when fed, behaves randomly on hearing S1, hides on hearing S2
<1,0,1,0> sounds S1 when fed, opens its mouth on hearing S1, behaves randomly on hearing S2
<1,0,1,1> sounds S1 when fed, opens its mouth on hearing either S1 or S2
<1,0,1,2> sounds S1 when fed, opens its mouth on hearing S1 and hides on hearing S2
<1,0,2,0> sounds S1 when fed, hides on hearing S1and behaves randomly on hearing S2
<1,0,2,1> sounds S1 when fed, hides on hearing S1but eats on hearing S2
<1,0,2,2> sounds S1 when fed, hides on hearing any sound
<1,1,0,0> sounds S1 when fed or hurt, behaves randomly on hearing any sound.
<1,1,0,1> sounds S1 when fed or hurt, behaves randomly on hearing S1, opens its mouth on hearing S2
<1,1,0,2> sounds S1 when fed or hurt, behaves randomly on hearing S1, hides on hearing S2
<1,1,1,0> sounds S1 when fed or hurt, opens its mouth on hearing S1, behaves randomly on hearing S2
<1,1,1,1> sounds S1 when fed or hurt, opens its mouth on hearing either S1 or S2
<1,1,1,2> sounds S1 when fed or hurt, opens its mouth on hearing S1 and hides on hearing S2
<1,1,2,0> sounds S1 when fed or hurt, hides on hearing S1 and behaves randomly on hearing S2
<1,1,2,1> sounds S1 when fed or hurt, hides on hearing S1 but eats on hearing S2
<1,1,2,2> sounds S1 when fed or hurt, hides on hearing any sound
<1,2,0,0> sounds S1 when fed and S2 when hurt, behaves randomly on hearing any sound.
<1,2,0,0> sounds S1 when fed and S2 when hurt, behaves randomly on hearing any sound.
<1,2,0,1> sounds S1 when fed and S2 when hurt, behaves randomly on hearing S1, opens its mouth on hearing S2
<1,2,0,2> sounds S1 when fed and S2 when hurt, behaves randomly on hearing S1, hides on hearing S2
<1,2,1,0> sounds S1 when fed and S2 when hurt, opens its mouth on hearing S1, behaves randomly on hearing S2
<1,2,1,1> sounds S1 when fed and S2 when hurt, opens its mouth on hearing either S1 or S2
<1,2,1,2> sounds S1 when fed and S2 when hurt, opens its mouth on hearing S1 and hides on hearing S2
<1,2,2,0> sounds S1 when fed and S2 when hurt, hides on hearing S1 and behaves randomly on hearing S2
<1,2,2,1> sounds S1 when fed and S2 when hurt, hides on hearing S1 but eats on hearing S2
<1,2,2,2> sounds S1 when fed and S2 when hurt, hides on hearing any sound .
<2,0,0,0> sounds S2 when fed, behaves randomly on hearing any sound
<2,0,0,1> sounds S2 when fed, behaves randomly on hearing S1, opens its mouth on hearing S2
<2,0,0,2> sounds S2 when fed, behaves randomly on hearing S1, hides on hearing S2
<2,0,1,0> sounds S2 when fed, opens its mouth on hearing S1, behaves randomly on hearing S2
<2,0,1,1> sounds S2 when fed, opens its mouth on hearing either S1 or S2
<2,0,1,2> sounds S2 when fed, opens its mouth on hearing S1 and hides on hearing S2
<2,0,2,0> sounds S2 when fed, hides on hearing S1 and behaves randomly on hearing S2
<2,0,2,1> sounds S2 when fed, hides on hearing S1 but eats on hearing S2
<2,0,2,2> sounds S2 when fed, hides on hearing any sound
<2,1,0,0> sounds S2 when fed, S1 when hurt, behaves randomly on hearing any sound.
<2,1,0,1> sounds S2 when fed, S1 when hurt, behaves randomly on hearing S1, opens its mouth on hearing S2
<2,1,0,2> sounds S2 when fed, S1 when hurt, behaves randomly on hearing S1, hides on hearing S2
<2,1,1,0> sounds S2 when fed, S1 when hurt, opens its mouth on hearing S1, behaves randomly on hearing S2
<2,1,1,1> sounds S2 when fed, S1 when hurt, opens its mouth on hearing either S1 or S2
<2,1,1,2> sounds S2 when fed, S1 when hurt, opens its mouth on hearing S1 and hides on hearing S2
<2,1,2,0> sounds S2 when fed, S1 when hurt, hides on hearing S1 and behaves randomly on hearing S2
<2,1,2,1> sounds S2 when fed, S1 when hurt, hides on hearing S1 but eats on hearing S2
<2,1,2,2> sounds S2 when fed, S1 when hurt, hides on hearing any sound
<2,2,0,0> sounds S2 when fed or hurt, behaves randomly on hearing any sound.
<2,2,0,0> sounds S2 when fed or hurt, behaves randomly on hearing any sound.
<2,2,0,1> sounds S2 when fed or hurt, behaves randomly on hearing S1, opens its mouth on hearing S2
<2,2,0,2> sounds S2 when fed or hurt, behaves randomly on hearing S1, hides on hearing S2
<2,2,1,0> sounds S2 when fed or hurt, opens its mouth on hearing S1, behaves randomly on hearing S2
<2,2,1,1> sounds S2 when fed or hurt, opens its mouth on hearing either S1 or S2
<2,2,1,2> sounds S2 when fed or hurt, opens its mouth on hearing S1 and hides on hearing S2
<2,2,2,0> sounds S2 when fed or hurt, hides on hearing S1 and behaves randomly on hearing S2
<2,2,2,1> sounds S2 when fed or hurt, hides on hearing S1 but eats on hearing S2
<2,2,2,2> sounds S2 when fed or hurt, hides on hearing any sound
Among these 81 strategies there are only two that we consider 'perfect communicators': strategies <1,2,1,2> and <2,1,2,1>. Strategy <1,2,1,2> makes sound S1 when fed and sound S2 when hurt, responding symmetrically to S1 by opening its mouth and to S2 by hiding. Strategy <2,1,2,1> follows the same pattern with sounds S1 and S2 interchanged.
Consider then a uniform field of 'perfect communicators' <1,2,1,2>. On successfully eating, a cell will make sound S1. Its neighbors, on hearing that sound, will open their mouths. Since food sources are migrating cell by cell in a random walk, with a probability of 1 in 9 of landing on any given neighbor cell, each neighbor cell that opens its mouth in response to an S1 signal will then increase its probability of gaining points by successfully feeding.(8) A similar pattern can be expected if neighbors hide in response to sound S2 when a cell is 'hurt' by a predator. A uniform field of strategy <2,1,2,1> would show the same advantages, using the alternative correlation between particular sounds and food or predation.
We term <1,2,1,2> and <2,1,2,1> 'perfect communicators' simply because of their behavioral symmetry with regard to the sounds they make and the sounds they respond to.(9) For present purposes our claims for communicative 'perfection' here go no further. 79 of the 81 strategies above fail of even that limited 'perfection' because they don't exhibit a sound-behavior symmetry across the full range of their behavioral repertoire. 'Free riders' constitute a special category of imperfect strategies, which seem to exploit communication received without responding with symmetrical communication in return. A 'free rider' may react to a particular sound by opening its mouth, for example-thereby benefitting from a neighbor's signal-but when fed will not send a corresponding signal from which its neighbor might benefit in return.
In our background study, before introducing recombination by way of genetic algorithm, we simply randomized all 81 strategies into our 64 x 64 array and allowed 50 food sources and 50 predators to wander as outlined. Figure 1 shows the look of our initial array, with strategies coded in terms of a black and white approximation to colors with contrasting central dots, a larger black square for an open mouth and a grey square for 'hiding'. Food items and predators are indicated by white dots, with sounds heard locally shown as a lightening of 3 x 3 squares of cells.

Fig. 1 Initial randomized array of 81 strategies, with food and predators shown as white dots and sounds heard locally shown as a lighter shade in 3 x 3 squares of cells.
In this background test we set both the gain for 'eating' and the loss for being 'hurt' by a predator at 1 point. Cells would accumulate points over a run of 100 rounds (a 'generation'). Before introducing the genetic algorithm, however, we changed strategies by simple replacement. After 100 rounds, each cell surveyed its immediate neighbors. If any neighbor had a higher score, it adopted the strategy of that neighbor with the highest. This follows the pattern of our previous work with simpler strategies. It allowed us time to check that the model was functioning as intended, as well as offering a base-line for comparison more complicated models intended to change strategies by genetic recombination.
Contrary to expectations, however, this background test showed a take-over by strategies <2,0,1,1> and <1,0,1,1>. Either or both might end up in possession, with only the randomness of initial configurations dictating which had the upper hand (Figure 2).

Fig. 2 Non-genetic 'replacement' with 50 food items and 50 predators: conquest by <1,0,1,1> and <2,0,1,1>. 600 generations shown.
Why did these two strategies conquer, rather than a 'perfect communicator' <1,2,1,2> or <2,1,2,1>?
What strategies <1,0,1,1> and <2,0,1,1> have in common is that they make some sound when eating and respond to any sound by opening their mouths. They thus speak essentially the same language-or 'sound 1' and 'sound 2' dialects of the same language-and so can respond to sounds of either strategy in their neighborhood by opening their mouths for eating. Both strategies show a clear preference for eating over hiding: both make sounds when eating, and respond to sound in terms of eating. Neither generates a sound when 'hurt' or responds to sound by hiding from predators. Why the preference for eating over hiding?
A bit of reflection on the dynamics of feeding and predation built into the model shows an important difference between the two. In an array composed entirely of 'communicators', a chain reaction can be expected in terms of food signals and successful feeding. One communicator signals that it has been fed, with the result that its neighbors open their mouths on the next round. The wandering food item then lands on one of neighbors (or the original cell), and that cell in turn makes a sound which signals its neighbors to open their mouths. One can watch a wandering food item cross an array of communicators, hitting an open mouth every time.
The dynamics of a 'hurt' alarm, on the other hand, are very different. Among even 'perfect communicators,' as specified, a cell communicates an alarm only when hurt-that is, when a predator is on him and he is not hiding. If successful, that 'alarm' will alert his neighbors to hide, and thus the predator will find no victim on the next round. Precisely because the predator then finds no victim, there will be no alarm sounded, and thus on the following round even a fellow 'communicator' may be hit by the predator. Here one sees not the chain reaction of successful feeding on every round but an alternating pattern of successful avoidance of predation every second round.
Our verdict on initial background runs, then, was that the dynamics of our model make the payoff for food great enough to swamp the relative disadvantage of predation. In such a model a cell is better served by opening its mouth whenever a neighbor makes any noise-since that may be the neighbor's signal for food-than distinguishing sounds in order to respond differently to a warning of predation.
We tested this hypothesis by repeating the runs with variations in the model. In a first variation, we had our cells send out an alarm when a predator was on them and whether or not they had their mouths open. In that variation, an alarm is sounded in the presence of a predator and even if no-one is actually hurt. With that change, a predation alarm should be able to spread in much the same pattern as a food announcement: a cell with a predator on it, hurt or not, will send an alarm which will allow his neighbors to avoid harm by hiding. They in turn will pass the alarm, whether or not they are actually hurt.
In a second variation, we kept the original model but simply doubled the number of predators. A greater number of predators, we reasoned, would increase the probability of being hit by predation and should therefore make avoidance of predators more important.
Both changes resulted in the expected conquest by our 'perfect communicators' <1,2,1,2> and <2,1,2,1> (Figures 3a and 3b). Here <1,0,1,1> or <2,0,1,1> continued to play a role as a third strategy, but each was eventually eliminated. Conquest in the end went to the 'perfect communicators' alone.
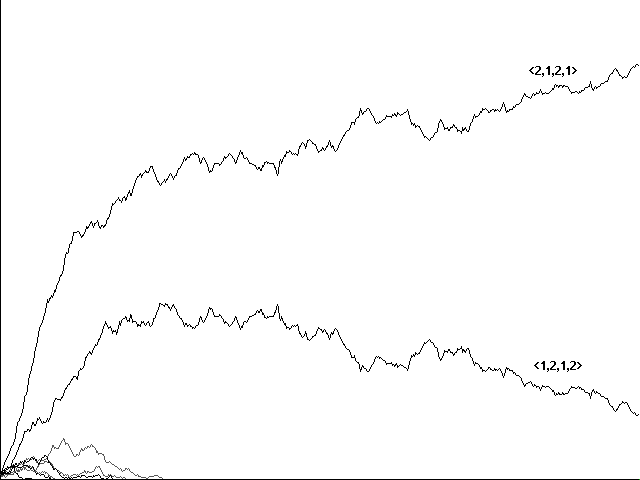
Fig. 3a Non-genetic 'replacement'. Conquest by 'perfect communicators' with 50 food items, 50 predators, and a 'predator on me' alarm instead of a 'hurt' alarm. 600 generations shown.
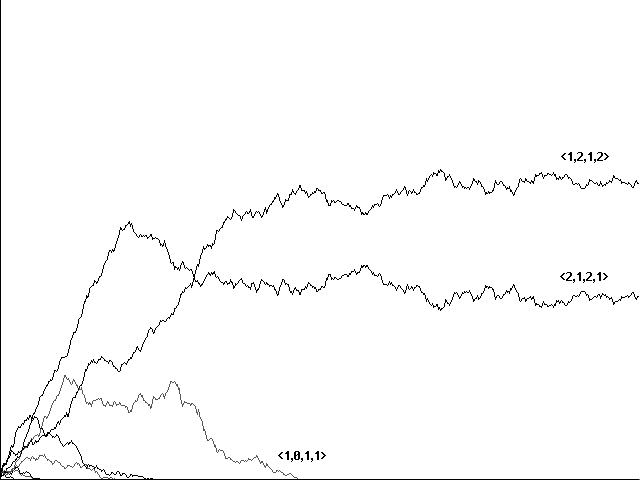
Fig. 3b Non-genetic 'replacement'. Conquest by 'perfect communicators' with 100 predators and 50 food items. 600 generations shown.
These background runs allowed us to test the basic form of our model prior to the introduction of strategy change by spatialized genetic algorithm. Although perfectly understandable in retrospect, one of the surprises was that the selective advantage of strategies of communication can depend on the content of the message conveyed. In a model even as simple as this one, despite identical gains for feeding and losses for predation, the different dynamics of feeding and predation may favor non-symmetric patterns of behavior regarding food and predators.
4. A Spatialized Genetic Algorithm Model for Evolution of Communication
Our background tests used strategies specified in terms of four ternary parameters. This offers a sample space of only 81 strategies, a number small enough for significant initial representation in a randomized 64 x 64 cellular array. Eventually, however, we wanted to consider more complicated strategies specified in terms of at least 6 ternary variables, giving us a sample space of 729 possible strategies. A sample space that includes that many strategies makes it much less appealing to randomize them all across a small initial array. With strategies dependent on coordination with neighbors-precisely the situation with communication-it is clear y that accidents of initial randomization are liable to swamp the effects of local selection for strategy success.
A model that starts instead with a small number of initial Adams and Eves, and in which successful strategies emerge through genetic recombination, solves this problem. One promise of localized genetic algorithms was therefore a model that would allow us to work with a larger sample space of more complicated strategies, still modeling strategy change in terms of local action within a spatialized array, but without forcing us to swamp an initial array with a randomization of all strategies at once.
It is also true, of course, that the use of localized genetic algorithms introduces a different dynamics for strategy change. In each of the runs below we start with a small number of Adams and Eves, chosen at random except that we quite deliberately weed out any strategies toward which we expect convergence. We deliberately avoid initial strategies that are in any way close to 'perfect communicators', for example. Sets of Adams and Eves are also chosen so that each possible variable (0, 1, or 2) will be represented in each variable position somewhere within the set. If we are working with 6 ternary variables, we make sure that values 0 through 2 are represented in each of our 6 positions somewhere among our initial population of strategies. Genetic recombination of the type at issue can eventuate in a strategy with a 2 in the final position, for example, only if one of the strategies it begins with has a 2 in that position. Without assurance that all values were at least possible in all positions we would be unable to explore major portions of the full strategy space at issue.
From that point on the genetic algorithm works as follows. Guided by results in our background tests, we begin with 50 food items and 100 predators. Each cell, after having accumulated a score from feeding and predation over the course of 100 rounds, surveys the scores of its immediate neighbors. If it has a neighbor with a higher score, it 'breeds': its strategy is changed to one that is a genetic cross between its previous strategy and that of its most successful neighbor.
Technically, this is done by choosing at random two points in the series of values that characterize the two strategies at issue: points 2 and 4 in a series of 6 values, for example. This gives us an 'inside' set of values-those between 2 and 4 inclusive, in this example-and an 'outside'. We then use the programming equivalent of flipping a coin. If the coin comes up heads, it is the 'inside' values of the original strategy that remain and the 'outside' values that are changed to those of its most successful neighbor. If the coin comes up tails, it is the 'outside' values that remain the same and the 'inside' values that are changed to those of its neighbor (Figure 4).
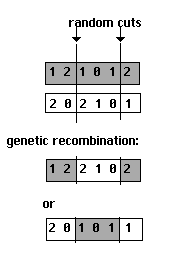
Fig. 4 General strategy of genetic recombination of strategies
'Breeding' or 'crossover' in genetic algorithms is often done using only one random point rather than two (see for example Holland 1992). One chooses a random spot at which to cut both strategies A and B, creating a new strategy that combines that section of A left of the random cut with that section of B right of the random cut, or vice versa. One consequence of this simpler mechanism for recombination, however, is that the ends of a strategy are treated differently from the middle. Consider the digits at the very ends of strategy A. With a single random cut, either of these digits may end up being the only element from A dropped into an otherwise different strategy. This does not hold for digits between the ends, which on a single cut will always reappear with at least one original neighbor. In choosing two points for cuts instead, including the possibility of a cut 'after the last digit', both this positional bias or 'end-effect' and other difficulties noted in the literature are significantly reduced (see Eshelman, Caruana, and Shaffer, 1989, and Mitchell 1996).
In the models developed below, all change in strategies follows this pattern for genetic recombination. At no point does any cell simply adopt the full strategy of a successful neighbor. A successful strategy, then, can be expected to contribute only part of its genetic code to those strategies that replace its less successful neighbors. Only by progressive approximation could a successful strategy be literally duplicated, and only by either being as successful as any strategy in its immediate neighborhood or by cross-breeding with a genetically identical neighbor could the strategy of any given cell remain unchanged. In the course of genetic recombination, we can expect a great number of different strategies to be produced, and these might or might not prove more successful than their neighbors. The result is a wide sampling across possible strategies through local action-precisely what we are after-despite the fact that we start with only a manageable handful of Adams and Eves.
A typical run on this basic pattern might progress as in Figure 5. We begin with a randomization of a small number of Adams and Eves across the array-in this case, only six. For the sake of clarity, Figure 5 shows only the strategies themselves, without displaying food items, predators, and sounds. Our initial six strategies quickly proliferate by genetic recombination, as shown in the second frame; here a wide range of different strategies are encoded by different combinations of background color and color of a central dot. In the course of the run, however, more successful strategies tend to form genetically uniform enclaves. With recombination always continuing at borders, more successful strategies emerge and progressively occupy greater percentages of the territory. An important point that simplified black and white illustration unfortunately obscures is that the dominant strategies that emerge to occupy large ranges of territory are entirely different from the Adams and Eves with which we began.




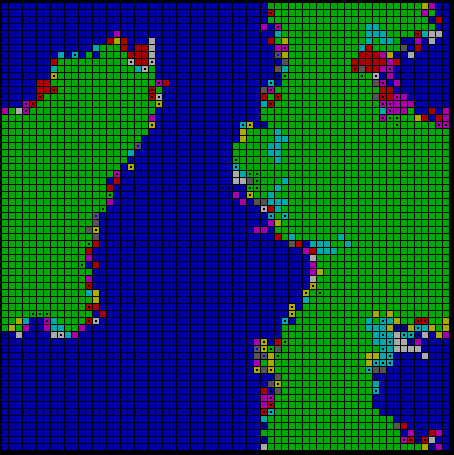
Fig. 5 Typical evolution of an spatialized array by genetic algorithm, starting with a random distribution of 6 Adams and Eves. Initial strategies quickly proliferate, eventually converging to a small number of successful strategies with continued genetic recombination at their borders.
In our background tests, using a randomized array of all 81 strategies that changed by pure 'replacement', we saw an eventual convergence to a field of 'perfect communicators'. Will the same hold true for an array that starts merely with a small set of Adams and Eves, with all changes in terms of genetic crossover instead? Can communicative strategies both arise by local genetic recombination and conquer in such an environment?
The answer is 'yes'. The three runs in Figure 6 start with different sets of Adams and Eves, and show varying number of generations. All show the progressive emergence of our two 'perfect communicators', however, with the eventual triumph of one.
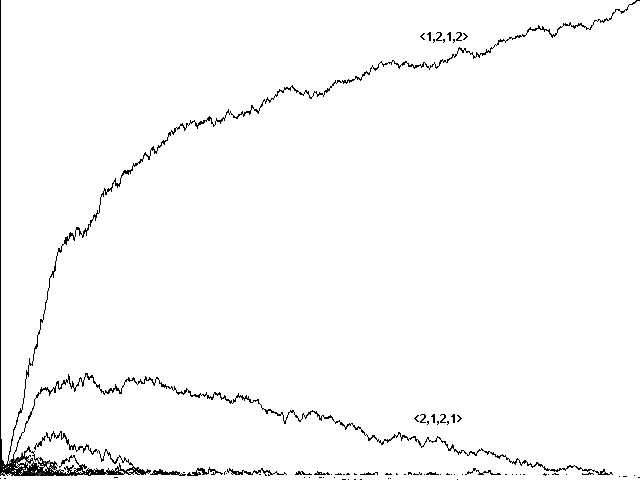
Fig. 6a Genetic algorithm evolution to a perfect communicator <1,2,1,2> over 1724 generations.
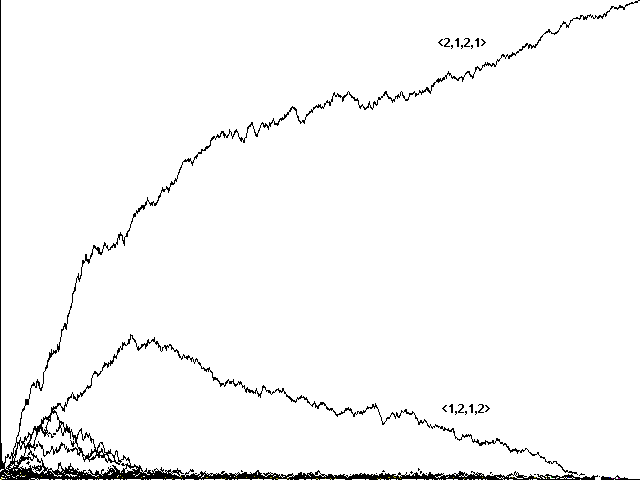
Fig. 6b Genetic algorithm evolution to a 'perfect communicator' <2,1,2,1>, over 1998 generations.
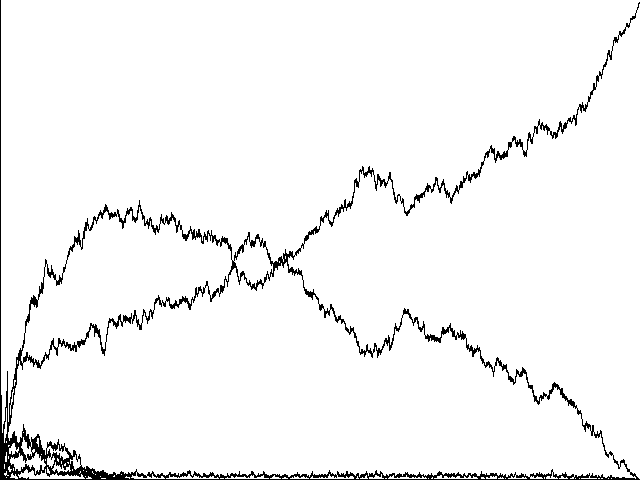
Fig. 6c Genetic algorithm evolution to a 'perfect communicator' <1,2,1,2>, over 5500 generations. Change in line quality is due to compression of the longer run.
5. Evolution of More Complex Communicative Strategies
Behavioral repertoires were expanded in a further model. In the runs above, individuals could only open their mouths or hide at any point. Our ternary coding represented the following possibilities in response to sound: that an individual opens its mouth, hides, or randomly chooses between the two.
In a further extension of the model we expanded behavioral repertoires to include a genuinely 'neutral' third alternative, allowing each individual the possibility of opening its mouth (appropriate for feeding), of hiding (appropriate for evading a predator), or of 'resting' in a neutral position. Our strategies were accordingly expanded to a field of 243 possibilities, coded as five-tuples <f, h, s1, s2, s>. Such a strategy specifies what the individual does when fed f or hurt h (make no sound, make sound S1, or make sound S2) and what it does when it hears a sound S1, a sound S2, or no sound at all (open its mouth, hide, or rest in neutral).
In this more developed model we also exacted a 'cost' or 'tax' of .02 points for opening one's mouth or for hiding, on the theory that these involve an expense in terms of energy. Gain for feeding and loss for predation were again set at 1 point. In 'open mouth' position an individual expends energy, therefore, can gain points for feeding, but will lose points if a predator lands on him. In 'hiding' position an individual expends energy, gains no points if food is present, but will avoid point loss from predation. The 'neutral' position carries no energy expense. In neutral an individual can gain no points for feeding, however, and will still lose points if a predator lands on him. We again used 50 more predators than food items, but increased the field to 75 food items and 125 predators in order to reduce computation time. Because of our greater number of strategy variables we started with 12 Adams and Eves, using the same technique of genetic recombination as before.
In this case the strategies that would qualify as 'perfect communicators' were <2,1,2,1,0> and <1,2,1,2,0>: each generates the same sound when feeding or when hurt as it responds to by opening its mouth or hiding. A zero in the last place indicates that these strategies adopt a purely neutral stance when they hear no sound from their immediate neighbors.
Does genetic recombination for these more complicated strategies still lead to evolution of perfect communicators and their eventual dominance in a population? Initial runs suggested a negative answer. Figure 7a, for example, shows a confused run toward <0,1,2,2,1>, <0,2,2,2,0>, <0,1,2,2,0>, and <0,2,2,2,1> in 10800 centuries. Figure 7b shows a similarly confused run toward the same strategies in 5761 centuries. In neither case did our 'perfect communicators' emerge and dominate.
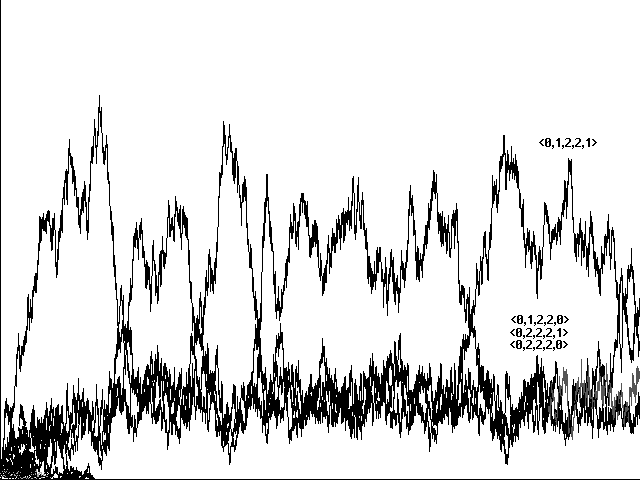
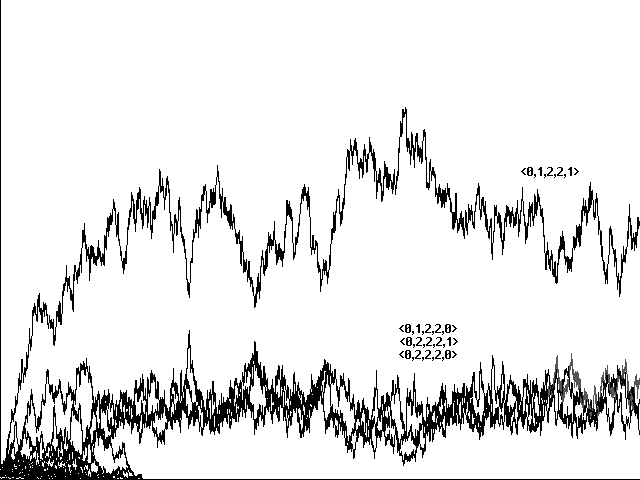
Why did 'perfect communicators' fail in this richer model?
In work on cooperation in the Prisoner's Dilemma, Nowak and Sigmund have shown evolutionary dynamics to be importantly different in 'perfect' and stochastically 'imperfect' worlds (Nowak and Sigmund 1990, 1992).(10) What their work introduces is the idea of worlds in which cooperation and defection, say, are always subject to some degree of uncertainty or stochastic noise. Our own earlier work had indicated an extension of Nowak and Sigmund's results to the case of communication, showing that simple communicative strategies can fail in a 'perfect' world and yet succeed in a stochastically 'imperfect' one (Grim, Kokalis, Tafti, and Kilb 1999).
With that precedent, we tried adding stochastic 'noise' to the current model as well. In this variation, each of a strategy's options were instantiated in only a probabilistically imperfect form. If a strategy <1,2,1,2,0> indicated a '1' for making sound S1 when fed, for example, we instantiated it with a 90% probability of making sound S1, a 5% probability of making sound S2, and a 5% probability of making no sound at all. All other strategy specifications were instantiated with similar imperfection. If a strategy specified a 'neutral' response when no sounds were heard, we gave it a 90% probability of neutrality, a 5% probability of opening its mouth, and a 5% probability of hiding.
Introducing that small measure of stochastic imperfection produced a significant change in the evolution of cooperation. Using precisely the same sets of Adams and Eves, and indeed the same initial configurations, runs now showed a slow but steady conquest by our 'perfect communicators' (Figures 8a and 8b). Here as in our earlier work, then, a measure of stochastic imperfection seems to play a positive role in the evolution of communication.
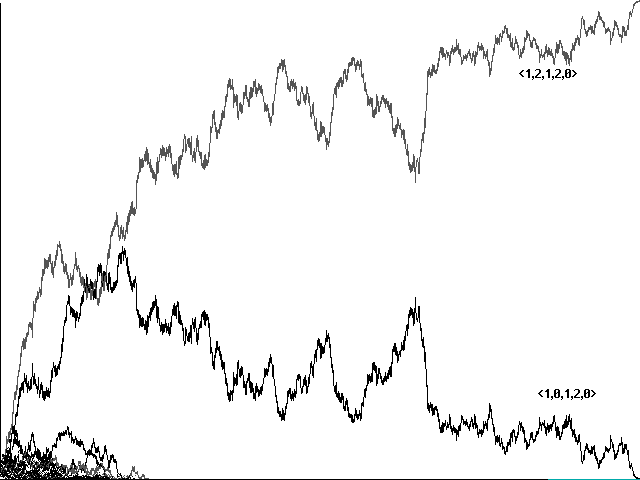
Fig. 8a Evolution to a perfect communicator in a stochastically imperfect world. 10800 centuries shown, using the same Adams and Eves and initial configuration as in 7a.
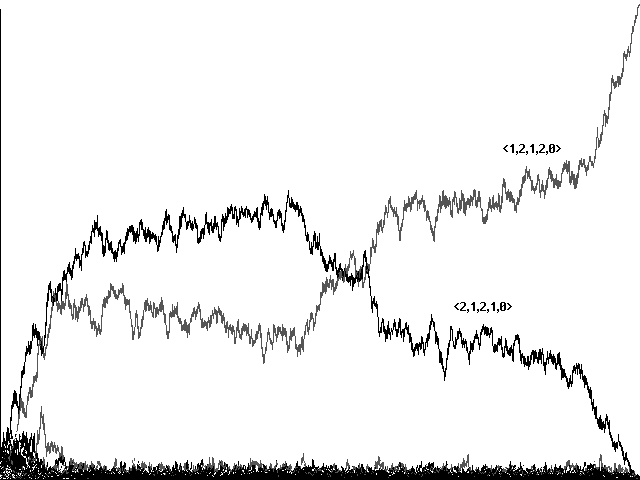
Fig. 8b Evolution to a perfect communicator in a stochastically imperfect world. 5761 centuries shown, using the same Adams and Eves and initial configuration as in 7b.
A significantly shorter run of 2364 centuries is shown in Figure 8c, using the same Adams and Eves as Figures 7b and 8b, the same stochastic imperfection, but starting from a different initial random configuration.
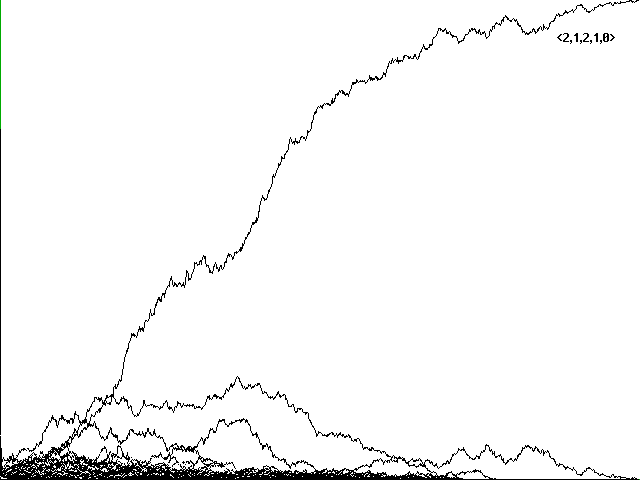
Fig. 8c Evolution to a perfect communicator in a stochastically imperfect world. 2364 centuries shown, using the same Adams and Eves as Fig. 7b but a different initial random configuration.
Why is it that communicative strategies fail in pure models but triumph in stochastically imperfect variations? The fundamental problem appears to be that 'perfect communicators' are disadvantaged in a perfect world by the fact that they cannot initiate successful communication on their own. A strategy of <1,2,1,2,0> responds to eating by making sound S1, heard by its neighbors. But it will open its mouth-the necessary prerequisite to eating-only if it hears sound S1 to begin with. In a perfect world, therefore, a uniform field of 'perfect communicators' <1,2,1,2,0> will never gain points by eating at all. No cell will have heard an initial sound S1 to make it open its mouth, so no cell will have an open mouth when food comes its way. Since it won't feed, it cannot generate any sound S1 to be heard by its neighbors.
This problem does not appear for predation. In a uniform field of strategies <1,2,1,2,0> there will initially be no sound. Because they hear no sound, all cells will be lingering in 'neutral', as dictated by the final '0' of their strategy. In 'neutral', however, cells remain vulnerable to attack by predators, and will therefore be 'hurt' by wandering predators. When hurt, their strategy dictates that they will make sound S2, which will then heard by their neighbors. Those neighbors will hide on the next round and thus avoid losing points from predation. Here as before the 'predation alarm' only avoids predation on every other round: a cell with strategy <1,2,1,2,0> which hides in response to hearing S2 will then avoid predation, but as a result will not give the warning S2 necessary to avoid predation on the following round.
Both of these theoretical points can be illustrated experimentally. If we seed our initial array entirely with <1,2,1,2,0> or <2,1,2,1,0>, we can track the random walk of predators through alternating rounds of predation, warning and hiding, and predation again. We can track a random walk of food items uniformly unannounced and uneaten.
In a world without stochastic imperfection, then, a 'perfect communicator' will be disadvantaged with regard to feeding. The problem will not be obvious in a heterogeneous array, because there will be surrounding strategies which do make sounds to which <1,2,1,2,0> or <2,1,2,1,0> will respond by opening their mouths and thus occasionally feeding. Once a member of either strategy does feed successfully, it will announce that fact using the sound represented by the first digit in its code, and the surrounding members of the same strategy will then be able to feed in turn. Without an initial stimulus from the sound of another strategy, however, feeding within a community of 'perfect communicators' can't even get started. Any pressure toward evolution of 'perfect communicators' will therefore be inherently limited. The larger the percentage of 'perfect communicators', the greater the problem of initial feeding will become; 'perfect communicators' in a perfect world cannot evolve to occupy the whole without producing a situation in which they can no longer gain points by feeding. On this scenario, the more successful strategies in stochastically perfect worlds should be those which use communication only to avoid predation: strategies that make a sound when hurt rather than when fed, and which respond to sound by hiding. The strategies with these characteristics are precisely those with initial digits 0,1,2,2, which show up as the uneasy competitors in Figures 7a and 7b.
The initial feeding problem for 'perfect communicators' is avoided in a stochastically 'imperfect' world. In such a world it will be possible for a 'perfect communicator' <1,2,1,2,0> to have its mouth open despite the fact that it has heard no sound, since each of our variables is instantiated with only 90% accuracy. In 5% of the cases in which it hears no sound, strategy <1,2,1,2,0> will open its mouth anyway. Should there happen to be food present at the time, it will successfully eat and will then make sound S1, triggering mouth-opening in its neighbors. The longer a run before recombination, the greater the efficiency in food consumption will be.
Why didn't this problem appear in the simpler models described in earlier sections? There our strategies had no neutral states. All cells were programmed, in the absence of any sound, for a random choice between opening their mouths and hiding. In those simpler models 'perfect communicators' therefore already had randomness built in, allowing them to avoid the initial feeding problem that arises here.
One conclusion at this stage is that more complicated strategies can bring with them unexpected complications of feeding and predation dynamics. The proportion of food items and predators used in these studies was carried over from background tests in which the alternating dynamics of predation proved important. Because strategies operate differently here, particularly in the absence of sound, those proportions may have different effects. In the cases above, we used 75 food items and 125 predators. For variations limited to 50 food items and 100 predators, still using a .02 tax for hiding or mouth-opening, communication does not succeed in even the stochastically imperfect case, presumably because the food resources are not high enough to compensate for the exertion tax on opening one's mouth. That result holds for models with 50 food items and 100 predators even if we reduce the tax to .01 in each case. If we raise the numbers of food items and predators to 100 and 150, on the other hand, we get similar results to those above but in significantly shorter runs: in a mere 2000 generations that set of Adams and Eves used in Figures 7a and 8a goes to <0,1,2,2,1> in a perfect world and to total success for the perfect communicator <1,2,1,2,0> in an stochastically imperfect world. In a modeling variation that uses an equal number of 100 food items and 100 predators results are less clear. This equal balance appears to constitute a threshold: with 100 food items and 100 predators we had runs in which one set of Adams and Eves went to 'perfect communicators' in the perfect world but not in the stochastically imperfect, while another set of Adams and Eves went to 'perfect communicators' in the stochastically imperfect world but not in the perfect.
6. Spatialized Genetic Algorithm Evolution of Communication with Six Variables
In a final series of experiments we expanded the model above to six-tuple strategies <, f, h, s1, s2, s>, with variables indicating what a cell does when neither fed nor hurt (make sound S1, make sound S2, or make no sound), what it does when fed f or hurt h (the same three options), and what it does when it hears sound S1, sound S2, or no sound s (open its mouth, hide, or 'rest' in neutral). With a sample space of 729 strategies, we started runs with an initial 18 Adams and Eves. Having learned our lesson, all models were run using stochastic imperfection. Where strategies indicate a '1' for making a sound, they in fact make that sound with a probability of 90%; options 0 and 2 appear in such a case with probabilities of 5% each.
Here as in the previous model a 'cost' or 'tax' of .02 points was exacted for opening one's mouth or for hiding. In this more complicated model we also exacted a 'tax' for making a sound, however, on the theory that an announcement of successful feeding, or a warning of predation, uses energy as well.(11)
Here our 'perfect communicators'-two strategies out of 729-are <0,2,1,2,1,0> and <0,1,2,1,2,0>. Can communication evolve in terms of a local genetic algorithm in this more complex environment as well? The answer is yes. Figures 9a and 9b show an evolution to a 'perfect communicator' in 2284 centuries and 1144 centuries, respectively, where we use 75 food items, 150 predators, a tax of .02 for opening one's mouth or hiding, and a tax of .01 for making either sound.
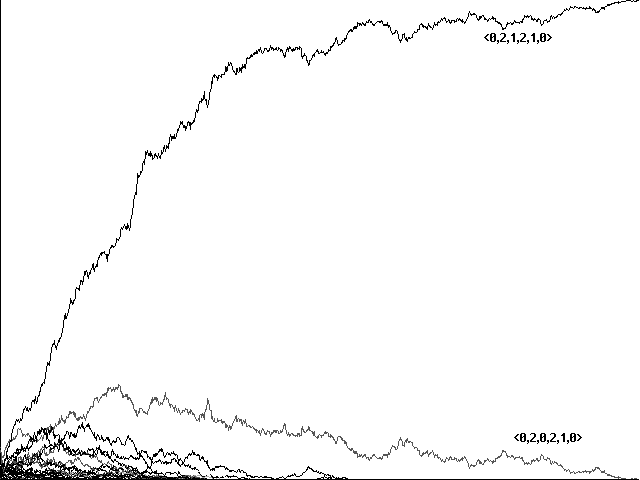
Fig. 9a Evolution to a 'perfect communicator' in 2284 centuries with 75 foods, 150 predators, .02 tax for action, .01 tax for sounding
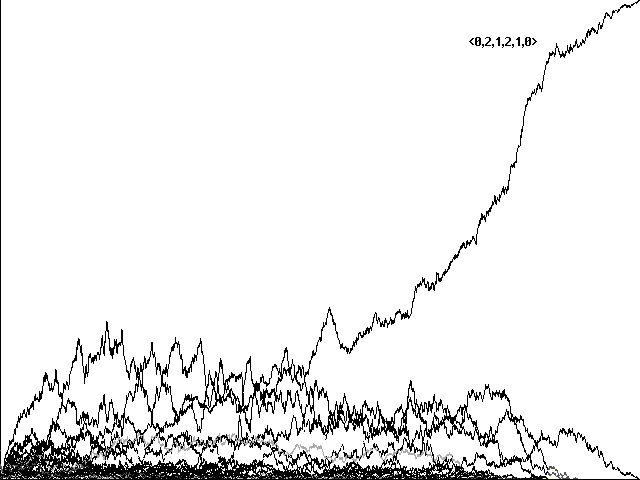
Fig. 9b Evolution to a 'perfect communicator' in 1144 centuries with different initial Adams and Eves, 75 foods, 150 predators, .02 tax for action, .01 tax for sounding
In a model this complicated, evolution to communication is sensitive both to proportions of food items and predators and to the level of 'tax' exacted for the making of sounds. In a variation with slightly fewer predators-125 instead of 150-evolution favors less than perfect communicators that concentrate on food announcements rather than on predator warnings. Runs shown in Figures 10a and 10b use the same Adams and Eves as Figures 9a and 9b, respectively, but show a continuing competition and symbiosis between <0,2,1,2,1,0> and <0,2,0,2,1,0>-a 'perfect communicator' and a less communicative 'shadow'-rather than a triumph by the 'perfect communicator' alone. It is indeed the shadow strategy <0,2,0,2,1,0> that is dominant in each case. In this ecology <0,2,0,2,1,0> avoids the tax of sounding a warning when hit by a predator, but it continues to benefit as a 'free rider' by responding to warning sounds from the companion strategy <0,2,1,2,1,0>. With slightly fewer predators and a significant population of communicators, it appears, the importance of a warning call among the shadow-strategy 'free riders' doesn't justify its energy cost.
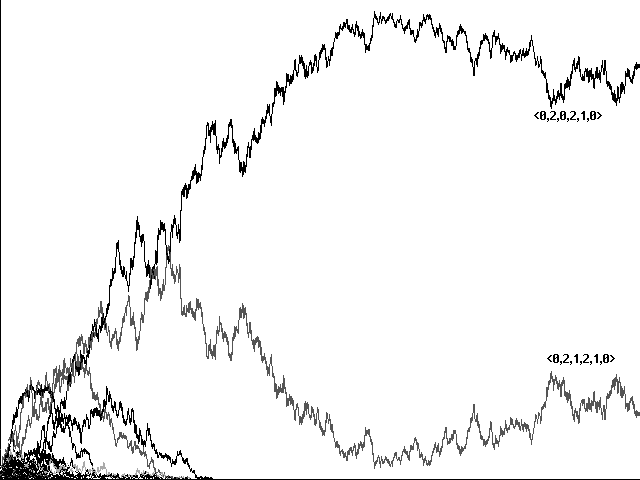
Fig. 10a Evolution to less than perfect communication in 5085 centuries with 125 predators. Same Adams and Eves Fig. 9a.
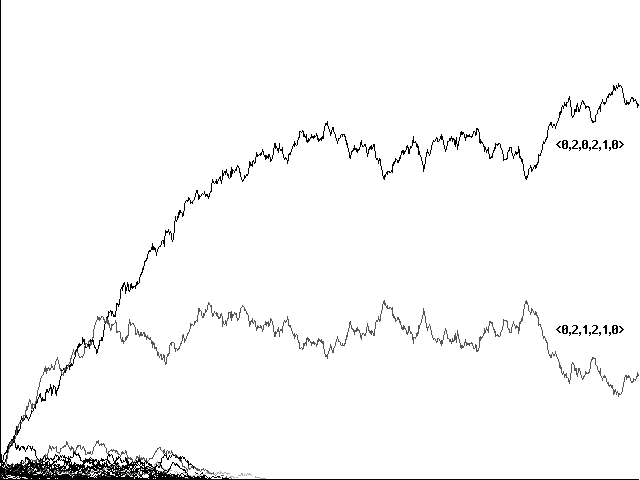
Fig. 10b Evolution to less than perfect communication in 1144 centuries with 125 predators. Same Adams and Eves as Fig. 9b.
Figures 11a and 11b show similar runs in which we kept food items at 75, predators at 150, but increased the tax for making sounds from .01 to .02. That change in energy expenditure was again enough to limit the evolution of communication. In the run shown in Figure 11a, using the same Adams and Eves as Figures 9a and 10a, evolution proceeds to both 'perfect communicators' <0,1,2,1,2,0> and <0,2,1,2,1,0> but is unable in 2284 centuries to eliminate the shadow 'free rider' <0,1,0,1,2,0>. By generation 3350, not shown, <0,1,0,1,2,0> in fact proves dominant. In the run shown in Figure 11b, using the same Adams and Eves as Figures 9b and 10b, evolution is dominated by the perfect communicator <0,2,1,2,1,0> but is unable in 1144 centuries to eliminate the shadow 'free rider' <0,2,0,2,1,0>.
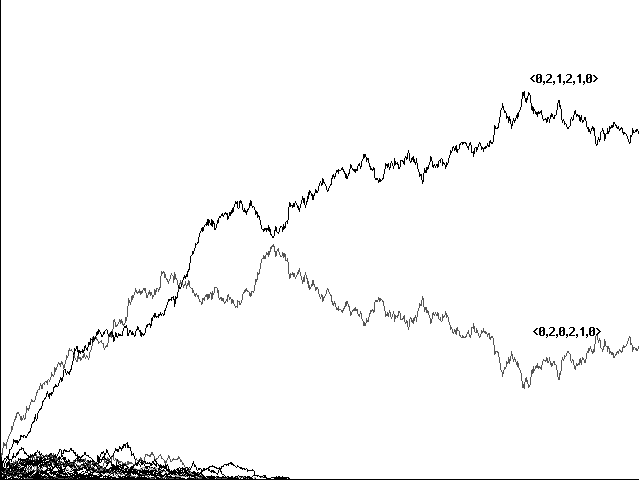
Fig. 11a Evolution to less than perfect communication in 2284 centuries with .02 tax on sounding. Same Adams and Eves as Figs. 9a, 10a.
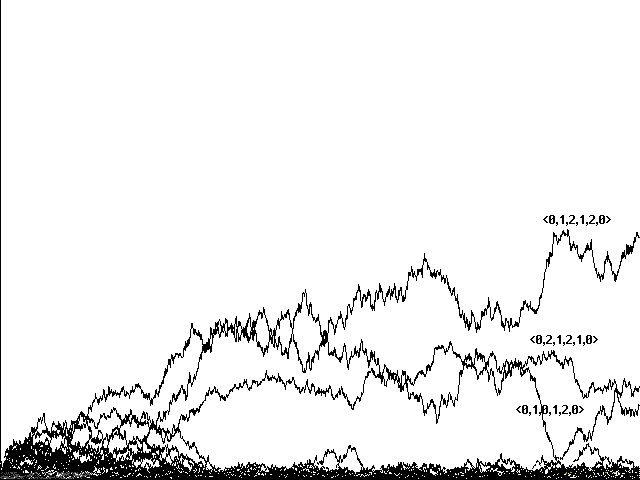
Fig. 11b Evolution to less than perfect communication in 1144 centuries with .02 tax on sounding. Same Adamss and Eves as Figs. 9b, 10b.
7. Conclusion
In earlier work we offered spatialized models to show that simple communication within a community can arise in a wide range of circumstances by mechanisms of evolutionary imitation. There, as in the background models of section 3 above, individuals simply adopt strategies that have proven successful among their immediate neighbors.
Our attempt here has been to replace that imitative mechanism with the strategy recombination of a localized genetic algorithm. At no stage in these more advanced models does any cell merely imitate a successful neighbor. At each stage it 'mixes' its strategy with that of its most successful neighbor instead. What this allows us is a fully spatialized model in which point maximization, communicative sound, and reproduction operate purely locally, but in which a significantly larger sample space of more complicated strategies can be studied.
Despite the wider range of more complicated strategies in such a model, and despite the lack of any pure imitation of success, evolution clearly proceeds to communities of 'perfect communicators' within a wide range of conditions. Here it is important that the costs of communication, either in generating signals or in responding to them, not be too high in comparison with potential gain from successful feeding and avoided loss from predation. It is also important that probabilities of gains and losses reflect the importantly different dynamics that emerge for feeding and predation. Here as in previous models it should be noted that communication succeeds only in a stochastically imperfect world in which at least some feeding occurs without direct prompting by communication. Given those conditions, however, it is clear that communication can effectively evolve and flourish using the recombinant mechanism of spatialized genetic algorithms.
It is tempting to jump from abstract models employing the mechanism of genetic algorithms to hypotheses linking language with physical genetics. We don't believe that such a jump is yet justified, however, and we are not suggesting that 'real-world' evolution of either simple signaling systems or complex languages must be understood literally in terms of genetics. The formal mechanism of genetic algorithms used here, though borrowed from chromosomal recombination, can be taken much more generally as an abstract model for one type of strategy recombination. Nothing ties that abstract model rigidly to physical genetics. In a particular environment, an individual may attempt not to copy a neighbor's strategy whole but to incorporate elements of locally successful strategies into his own. The general form of recombinant algorithm employed here might thus be read as a form of 'meme' recombination rather than evolution in terms of literally physical genes (Dawkins 1976).
In combination with earlier studies, what the work above may suggest is that evolution of communication is not in fact limited to any particular mechanism of strategy reproduction. Simple patterns of communication may arise in models using very different basic mechanisms of strategy change. What we want to suggest is thus not that evolution of communication demands genetic recombination but that it is capable of exploiting that pattern of strategy change just as it is capable of exploiting others. We consider our models another piece of evidence that communication may arise easily and apparently spontaneously in a wide range of circumstances and using quite disparate mechanisms.
Life, it has sometimes been speculated, is not preciously rare but quite nearly inevitable. The same may be true of communication.
References
Ackley, D., and Littman, M., 1994. Altruism in the Evolution of Communication. In Rodney A. Brooks and Pattie Maes, eds., Artificial Life IV: Proceedings of the Fourth International Workshop on the Synthesis and Simulation of Living Systems (MIT Press), 40-48.
Batali, J., unpublished. Small Signaling Systems can Evolve in the Absence of Benefit to the Information Sender.
Cangelosi, A., and Parisi, D., 1998. The emergence of a 'Language' in an Evolving Population of Neural Networks. Connection Science 10, 83-97.
Dawkins, S., 1976. The Selfish Gene (Oxford University Press).
Dewdney, A., 1995. The Evolution of Flibs, Scientific American, November 1985, reprinted in
Dewdney, The Armchair Universe (W. H. Freeman, 1988).
Eshelman, L., Caruana, R., and Shaffer, J., 1989. Biases in the crossover landscape. In J. D. Schaffer, ed., Proceedings of the Third International Conference on Genetic Algorithms. (Morgan Kaufmann).
Grim, P., 1995. Greater Generosity in the Spatialized Prisoner's Dilemma, Journal of Theoretical Biology 173, 353-359.
Grim, P., 1996. Spatialization and Greater Generosity in the Stochastic Prisoner's Dilemma, BioSystems 37, 3-17.
Grim, P., Kokalis, T., Tafti, A., and Kilb, N., 1999. Evolution of Communication in Perfect and Imperfect Worlds. Research Report #99-01, Group for Logic and Formal Semantics. Forthcoming in World Futures: The Journal of General Evolution.
Grim, P., Mar, G., and St. Denis, P., 1998. The Philosophical Computer: Exploratory Essays in Philosophical Computer Modeling (MIT Press/Bradford Books).
Holland, J., 1992. Adaptation in Natural and Artificial Systems (MIT Press/Bradford Books).
Hutchins, E., and Hazlehurst, B., 1995. How to invent a lexicon: the development of shared symbols in interaction. In N. Gilbert and R. Conte, eds., Artificial Societies: The Computer Simulation of Social Life (UCL Press), 157-189.
Levin, Michael, 1995. The evolution of understanding: A genetic algorithm model of the evolution of communication. BioSystems 36 (1995), 167-178.
Lewis, David, 1969. Convention (Harvard University Press).
MacLennan, B., 1991. Synthetic Ethology: An approach to the study of communication. In C. G. Langton, C. Taylor, J. D. Farmer, and S. Rasmussen, eds., Artificial Life II, SFI Studies in the Sciences of Complexity, vol. X (Addison-Wesley), 631-655.
MacLennan, B., and Burghardt, G., 1994. Synthetic Ethology and the Evolution of Cooperative Communication. Adaptive Behavior 2, 161-188.
Mitchell, M., Hraber, P., and Crutchfield, J., 1993. Revisiting the edge of chaos: Evolving cellular automata to perform computations. Complex Systems 7, 89-130.
Mitchell, M., Crutchfield, J., and Hraber, P., 1994. Evolving cellular automata to perform computations: Mechanisms and impediments. Physica D 75, 361-369.
Mitchell, M., Crutchfield, J., and Das, R., 1997. Evolving cellular automata to perform computations. In Bäck, T., Fogel, D., and Michaelewicz, Z., eds., Handbook of Evolutionary Computation (Oxford Univ. Press).
Mitchell, M., 1996. An Introduction to Genetic Algorithms (MIT Press).
Nowak, M., and Sigmund, K., 1990. The evolution of stochastic strategies in the prisoner's dilemma. Acta Applicandae Mathematicae 20, 247-265.
Nowak, M., and Sigmund, K., 1992, Tit for tat in heterogeneous populations. Nature 355, 250-252.
Oliphant, M., and Batali, J., 1997. Learning and the Emergence of Coordinated Communication. Center for Research on Language Newsletter 11(1).
Skyrms, B., 1996. Evolution of the Social Contract (Cambridge University Press).
Steels, L., 1996. Emergent Adaptive Lexicons. In P. Maes, M.. Mataric, J. Meyer, J. Pollack and S. Wilson, From Animals to Animats 4: Proceedings of the Fourth International Conference on Simulation of Adaptive Behavior (MIT Press).
Steels, L., 1997. Synthesising the origins of language and meaning using co-evolution, self-organisation and level formation. In J. Hurford, ed., Evolution of Human Language (Edinburgh Univ. Press).
Wagner, K., forthcoming. Cooperative Strategies and the Evolution of Communication. Artificial Life, Vol. 6, Issue 2, MIT Press.
Notes
1. A similar background motivation, though with an entirely different implementation, is evident in Steels 1996 and 1997.
2. This is in turn a development of spatialized models for cooperation rather than communication that appear in Grim 1995, Grim 1996, and Grim, Mar, and St. Denis 1998.
3. The major interest of Grim, Kokalis, Tafti, and Kilb 1999 is that non-stochastic versions of such simple strategies did not show an advantage for communication. Within that simple model, at least, a stochastically imperfect world seemed to be required for the evolution of communication. A related result for the current models is discussed in section 5 below.
4. This difficulty in communication studies isn't limited to those employing genetic algorithms, of course; a similar limitation is evident in Hutchins and Hazlehurst 1995.
5. Werner and Dyer 1991 also suffers from the limitation noted above, modeling communication as a process which somehow rewards both sender and receiver simultaneously.
6. The idea of purely local reproduction in terms of genetic algorithms first came to our attention through the work of Paul St. Denis, developed in chapter 5 of Grim, Mar, and St. Denis 1998. In this model genetic algorithms are used as the mode of local strategy change within cellular automata. An entirely different combination of genetic algorithms and cellular automata appears in Mitchell, Hraber, and Crutchfield 1993, Mitchell, Crutchfield, and Hraber, 1994, and Mitchell, Crutchfield, and Das 1997. In their work genetic algorithms are used to select for rule sets which are then applied uniformly across one-dimensional cellular automata with certain computational goals in mind.
7. The fact that strategies default to a random choice of opening their mouths or hiding builds in a clear element of randomness which distinguishes this aspect of the current study from that in Grim, Kokalis, Tafti, and Kilb, 1999. That study had no predators. Cells would either open their mouths or not, with a closed mouth as the default. Within those parameters, we found, it was necessary to introduce an element of stochastic imperfection in order for communication to succeed. Here, on the other hand, simple coding for two behavioral options in the basic model includes a default randomness which creates the essentials of a stochastically imperfect world.
8. The probability is 1 in 9 rather than 1 in 8 because the random walk of a food source from a particular cell may put it on any of the eight neighboring cells at the next step or on the central cell again.
9. This behavioral symmetry, interestingly enough, seems to correspond quite closely to Saussure's 1916 notion of the bidirectionality of linguistic signs. See also Oliphant and Batali 1997.
10. This result also carried over to spatialized contexts. See Grim 1995, Grim 1996, and Grim, Mar, and St. Denis 1998.
11. An intriguing variation we did not pursue here would be one in which sound-making also increased the probability of predation.