![[Figure
1.]](fig-1t.gif)
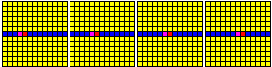
Figure 1. Conquest by TFT in a random array of 8 simple strategies.
Patrick Grim
pgrim@ccmail.sunysb.edu
see also "The Undecidability of the Spatialized Prisoner's Dilemma," Theory and Decision 42 (1997), 53-80
Group for Logic and Formal Semantics
Department of Philosophy
SUNY at Stony Brook
Stony Brook, NY 11794 USA
A version of this paper was presented at the IEEE International Conference on Computational Intelligence, combined meeting of ICNN, FUZZ-IEEE, and ICEC, Orlando, June-July, 1994, and an earlier form of the result is to appear as "The Undecidability of the Spatialized Prisoner's Dilemma" in Theory and Decision. An interactive form of the paper, in which figures are called up as evolving arrays of cellular automata, is available on DOS disk as Research Report #94-04i. An expanded version appears as chapter 6 of The Philosophical Computer.
Last modified 18 December 1995 by Robert Rothenburg Walking-Owl <wlkngowl@unix.asb.com>. Note: for reasons of browser and bandwidth friendliness, most of the imbedded images were reduced to thumbnails of 1/16th or 1/8th their original sizes. Clicking on the thumbnails will download larger versions of the images. For browsers that cannot handle the tables, there are links to ASCII text representations of them. (Many thanks to Andrew Faskowitz <afaskowi@ic.sunysb.edu> for implementation advice.)
Table of Contents:
Undecidability as it appears in Gödel's first theorem has a well-deserved reputation as a solid mathematical result with tantalizing philosophical overtones. But for most purposes Gödelian undecidability has also seemed fairly safe. What we're talking about, after all, is a result regarding axiomatic arithmetic. Despite what some philosophers of mathematics seem to think, axiomatic arithmetic is hardly the everyday stuff of applied or most pure mathematics, and is certainly not the everyday stuff of mathematical modelling in physics, engineering, economics, or theoretical biology. Gödelian undecidability, therefore, has earned a reputation as mathematically solid, philosophically tantalizing, but conveniently safe--a phenomenon safely distant in the icy regions of axiomatic arithmetic.
In what follows I want to outline and discuss a recent result which brings undecidability a little closer and therefore makes Gödel seem less safe. In so doing I think of myself as simply continuing a tradition which has progressively made Gödelian concerns seem less remote and less safe--a tradition including Turing's results in formal machine theory, Rice's theorem in recursion theory, and Chaitin's theorem in information theory.
Here classical undecidability is brought as close as the Prisoner's Dilemma, a standard paradigm of game theory. That's coming pretty close. In the last twenty years the Prisoner's Dilemma has established itself as a central model within theoretical biology and economics. If Gödelian undecidability shows up here, it shows up in even our simplest attempts to understand ourselves as biological and social organisms.
What I want to do, then, is:Since von Neumann, the Prisoner's Dilemma has been exhibit A within game theory.
Let us play a single round of the Prisoner's Dilemma, you and I. On that round each of us chooses one of two options-- to cooperate (C) or defect (D). How much each of us wins on the round depends on how both choices, by both players, come out.
The standard matrix is the following:
| me | ||||
|---|---|---|---|---|
| cooperate (C) | defect (D) | |||
| you | cooperate (C) | (3,3) | (you,me) (0,5) | |
| defect (D) | (you,me) (5,0) | (1,1) | ||
If we both cooperate, we both get 3 points. That's pretty good--a lot better than if we both defect, say, and walk away with only 1 point each. But the best outcome for me is if I can somehow sucker you into cooperating while I defect on you. In that case you end up with 0 and I walk away with 5 points.
This simple game-theoretic model seems to capture in miniature something of the tensions between individual acquisitiveness and the goals of collective cooperation. That is of course precisely why it has become a major focus of modelling within theoretical sociology, theoretical biology, and economics.
The Prisoner's Dilemma becomes both more interesting and more realistic as a model when it is made open-ended: when you and I engage in repeated games, never knowing whether we might meet again. In the Iterated Prisoner's Dilemma competing strategies emerge, including for example a vicious strategy of universal defection (AllD), or a come-on initial cooperation followed thereafter by vicious defection (C-then-AllD). The strategy called Tit for Tat (TFT) cooperates on the first round and thereafter simply repeats its opponent's play on the previous round. Tit for Tat has established a reputation on both experimental and theoretical grounds as particularly robust (Axelrod 1980a, 1980b, 1984; Axelrod and Hamilton 1981).
Over the past twenty years, our primary models for the evolution of cooperation in a community of self-serving egoists, in either a biological or social instantiation, have been written in terms of the Iterated Prisoner's Dilemma. It is no simplification to say that our strongest and simplest models of the evolution of biological and sociological cooperation--and in that respect our strongest and simplest models of important aspects of ourselves as biological and social organisms--are written in terms of the Iterated Prisoner's Dilemma.
In the Spatialized Prisoner's Dilemma a further dimension is added: that of space. Players with different strategies are envisaged as competing against immediate neighbors in a two-dimensional field. Each player in such a display competes with each of its neighbors in an iterated Prisoner's Dilemma and totals its scores from those competitions.[1] It then surveys its neighbors. If no neighbor has a higher local score, the player retains its original strategy. If it has a neighbor or neighbors with higher scores, on the other hand, it converts to the strategy of its most successful neighbor. The result is a model in which success is in all cases calculated against local competitors, with replication proceeding locally as well--both features which constitute a measure of realism with regard to either biological or sociological applications.
Fields of strategies in the Spatialized Prisoner's Dilemma evolve in the manner of cellular automata (Wolfram 1984; Toffoli and Margolus, 1987; Demongeot, Golés, and Tchuente, 1989; see also Nowak and May, 1992, 1993; Mar and St. Denis, 1993; and Grim 1993). Figure 1, for example, shows a typical evolution of a randomized field of eight simple strategies.
![[Figure
1.]](fig-1t.gif)
The viciously defecting strategies, shown in white and dark grey, are the early winners. As these threaten to take over, however, black clusters of TFT grow and thrive. In the end it is TFT which conquers all other strategies, ultimately occupying the field alone; by the twenty-sixth generation the screen is entirely black.
Undecidability of Spatialized Prisoner's
Dilemma
Does TFT always win? No: there is a clear sensitive dependence on initial conditions. Figure 2 (below) shows an arrangement of the same eight strategies, in the same proportions and appearing equally random, which results in a quick death for TFT and complete conquest by its vicious competitors.
![[Figure 2.]](fig-2t.gif)
A question often arises with regard to arrays of strategies whether one or another strategy will grow to conquest (TFT or AllD, say) or whether some equilibrium between various strategies will be established. With genuinely infinite arrays in mind, rather than computer-limited finite displays, the question might be posed as follows.
Let us suppose a standard infinite background--in the simplest case, an infinite sea of a single strategy. Into this sea we drop a smaller finite configuration of strategies: a patchwork island in the infinite sea (Figure 3).
![[Figure
3.]](fig-3t.gif)
The result is bound to be different in different cases. Some finite configurations dropped into our infinite sea may result in progressive conquest by a single strategy, dominating its neighbors and expanding ever outward. Some configurations may do something entirely different-- disappear completely, for example, reach a point of static equilibrium, or pulse periodically through cycles of expansion and contraction.
Here is the central question of the paper: For any chosen background, is there an algorithm which will tell us in each case what the result of embedding a certain finite configuration will be?
The work I want to outline here answers this question firmly in the negative. There is no general algorithm, computer program, effective procedure or step-by-step computation which will in each case tell us, for example, whether or not a given configuration of Prisoner's Dilemma strategies embedded in a uniform background will result in progressive conquest. [2] Despite the fact that it is one of the simplest models available for basic elements of biological and social interaction, the Spatialized Prisoner's Dilemma proves formally undecidable in the classical Gödelian sense.
Here I will just sketch the basic moves of the proof, leaving a more detailed presentation to another context.
In the first step, we start by considering a basic abstract machine. One form of the proof uses a close variant of a Turing machine. The form I'll outline here uses a Minsky register machine instead.
The basic structure of a Minsky register machine is that of a computational center connected to two memory registers (Figure 4, below). The memory registers replace the familiar Turing tape, and can be thought of as storage pits, each of which is capable of storing a single arbitrarily large integer. In place of the tape reading-and writing- abilities of standard Turing machines, we require only that the computational core of the machine be capable of adding a single unit to a register, of subtracting a unit, and of checking whether there a register has anything in it at all--whether its contents are zero. Given Church's Thesis, any computable function whatsoever is computable by some Turing machine. As Minsky showed long ago, any Turing machine can be simulated by a register machine, and thus any Turing-machine-computable function is Minsky-register-machine-computable as well.
![[Figure 4.]](fig-4.gif)
The particular forms of Minsky machines I have in mind here are wired. If we opened up the computational unit, in other words, what we'd see would be some finite tangle of wires. All we really need to demand of such wires, however, is that something called electrons travels along them at a standard rate. No other genuinely electrical properties will be required.
Within a computational unit such wires will turn corners and cross each other either with interaction or without. Some wire configurations can be expected to function as diodes, allowing electron motion in one direction along a wire but not another. These in turn may form part of the construction of or and not gates. It has long been clear that this small handful of elements offers a complete base for Boolean functions of any number of variables; with any form of wires capable of forming these basic elements we can rest assured that some configuration will serve the non-memory functions of any computational unit we might desire.
Can the memory registers of a Minsky machine be wired as well--can these be constructed in terms of electrons travelling along wires? In the sense required for the proof, the answer is "yes", though details are somewhat complex. You'll see them in a minute. For now I ask you to trust me: in the sense we will require, Minsky register machines can indeed be wired.
Minsky register machines, we've said, are equivalent to standard Turing machines. With that parallel, of course, comes a parallel to the standard Halting Problem. Rather than rehearse the full Halting Problem in terms of these particular abstract machines, however, let me offer a simpler presentation of the basic issue of undecidability along lines sketched by John Conway (Berlekamp, Conway, and Guy, 1982):
We know that either a Turing machine or a Minsky register machine can be constructed for the express purpose of investigating any explicitly specified, and arbitrarily hard, arithmetical question. We might construct a Minsky machine to search for counter-examples to Goldbach's conjecture, for example-- that every even number greater than 2 is the sum of two primes. Programmed to move even number by even number, checking alternative sums, our machine could be designed to indicate that it has found a counter-example by, say, sending a single pulse down a designated signal wire.
We can then envisage a range of machines, for a range of purposes, built with convenient signal wires. Our Goldbach machine, a carefully designed pattern of wires, is to send a pulse down its signal wire when a counter-example to Goldbach's conjecture is found. Our Fermat machine is to send a pulse down its signal wire if and when it reaches a set of values satisfying the familiar Fermat equation.
Because Minsky register machines are distinguished one from another by the finite contents of their computational unit, they can be listed, or enumerated, on that basis. They can, in effect, be 'coded' by their central wiring diagrams, and we can compile a list of them in terms of those wiring codes alone. Machines with auxiliary signal wires simply form a partial list.
The crucial question, however, is this: Is there a single algorithm which will tell us, for any machine on the list, whether it will or will not eventually send a pulse down its signal wire? The answer is "no". If there were such an algorithm, it would effectively tell us whether arbitrary difficult arithmetical problems have solutions. We've long ago proved that there is no technique bound to tell us when arbitrary arithmetical problems have solutions. There can thus be no general algorithm which predicts in each case the behavior of our abstract machines.
The first step of the proof, then, is a fairly standard undecidability result for a particular class of abstract machines. The second step takes us from abstract machines to a particular type of cellular automata. This is actually the bridge step of the proof. What we want to establish is that a particular type of cellular automata can simulate the behavior of the wires outlined for our abstract machines--and thus that abstract machines of this type can in effect be embedded in cellular automata arrays. The "particular type" of cellular automata at issue is one that will eventually tie in with the Spatialized Prisoner's Dilemma.
The idea of embedding wire-like behavior within cellular automata first appears (as far as I know) in a program A. K. Dewdney has dubbed Wirewor ld, developed by Brian Silverman of Logo Computer Systems (Silverman, 1987; Dewdney, 1990). Here our cellular automata environment is more complex, but the basic idea is the same: to simulate within cellular automata electron travel along wires, wire crossings, diodes and ultimately a complete base of Boolean gates.
The cells of our automata carry different colors for different strategies. Each cell is thought of as using that strategy in competition against its neighbors, adding those scores together for a total. In a second conceptual step a cell then compares its totals core with that of the cells around them. Should a neighboring cell have a higher local score it adopts that strategy, changing color in the process.
The following set of game scores, arrived at by the simple expedient of excruciating and laborious experimentation, gives us an operating wire-like simulation for four basic colors:
| strategy | |||||
|---|---|---|---|---|---|
| blue | red | purple | yellow | ||
| competitor | blue | 2.412 | 2.485 | 2.583 | 0.868 |
| red | 2.534 | 2.412 | 2.567 | 0.868 | |
| purple | 3.000 | 2.542 | 2.412 | 0.868 | |
| yellow | 2.472 | 2.472 | 2.472 | 2.667 | |
Figure 5 shows the simulation of electron travel along a wire. The reality, of course, is a static array of players which change colors in accord with competitive advantage. What is thereby simulated, however, is inescapably seen as movement.
What's happening is that the score for a red flanked by six yellows, a blue and a pink is higher than the score for the blue cell to its right. That blue cell then converts to red. At the same time, the score for our original red is less than that for the pink to its left, and it converts to pink. That pink scores less than the blue to its left, and so it converts to blue. An electron composed of a red head and pink tail seems to move progressively along a blue wire against a yellow background.
The scores shown above have been selected so as to satisfy a crucial sensitivity of blue squares to red, fine-tuned enough to allow both for electron branching and for a kill function used as a basic element in diodes and fundamental operators. Figure 6 (below), for example, shows a diode which allows electron travel left to right but blocks it by self-extinction right to left.
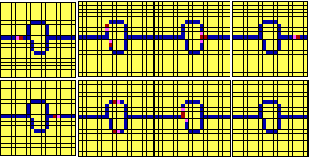
Figure 7 (below) shows a wire crossing. An electron can travel north to south without propagating to cause interference east or west, or can travel west to east without propagating north or south.
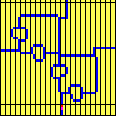
Or and not gates, finally, are shown in Figure 8: [3]

With these basic elements we can simulate, within competitive cellular automata, any finite arrangement of wires and standard gates. There will therefore be finite configurations of cells which will correspond to the computational units of any chosen Minsky register machines.
What of the Minsky registers? If registers are to grow with addition and shrink with subtraction, the four basic players and the short list of strategies above prove insufficient. A larger group of players defined in terms of a larger group of competitive scores, however-- giving us in effect a group of special electrons to serve the special purposes of wire growing and shrinking-- does allow for the full instantiation of Minsky register machines within two-dimensional cellular automata arrays (Table 3).
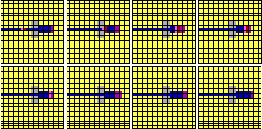
Figure 9 shows an instantiation of a Minsky register and exhibits the basic process of addition; you'll note that the fat segment grows one unit to the right.
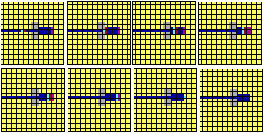
Figure 10 shows the basic mechanism of subtraction: the fat segment shrinks one unit.
In Figure 11 (below) is sketched a schematic of the register and its control mechanism as a whole-- a control mechanism which effectively converts timed normal electrons from the computational core to the special electrons required to regulate the registers.

Although details get complicated, the point is simply that any Minsky register machine can effectively be wired within competitive cellular automata. One of the nice things about Minsky machines, moreover, is that they are elegantly self-contained. Memory registers can start at zero and the machine as a whole can thus be instantiated as a finite configuration of strategies dropped into an unbroken infinite yellow sea of our background strategy.
So is there any step-by-step procedure--any algorithm--which will tell us in each case what the result of embedding a finite configuration of strategies in a sea of yellow will be? No, because among those finite configurations will be configurations which instantiate arbitrary Minsky register machines.
We can also make undecidability a bit more graphic. By adding two additional strategies, with appropriate scores, we can build a strategy bomb: a device which will keep hostage and harmless a small patch of one strategy-- bright green, say-- unless a pulse is sent down a particular wire. Given a pulse down that wire, on the other hand, bright green will be released to expand without obstacle ever outward, progressively conquering all strategies in its path (Figure 12, below).
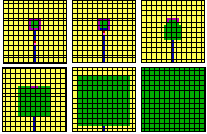
Consider now arbitrary finite arrangements of the strategies we've mentioned. Is there any algorithm or effective procedure which will tell us in each case whether the result will be a progressive conquest by bright green or not?
No. Minsky register configurations, we know, can be constructed to look for solutions to arbitrarily hard arithmetical problems. Suitably wired to strategy bombs, those machines can be instantiated as arrays of competitive cellular automata. Thus to arbitrarily difficult arithmetical problems will correspond arrays of strategies which will or will not result in progressive conquest by acid green depending on the solution to the problem at issue.
Were there an algorithm which sorted the relevant arrangements into those which would result in conquest and those which would not, therefore, there would also be an algorithm suitable for deciding arbitrarily difficult arithmetical problems. We know there can be no algorithm of that sort, and thus that there can be no algorithm of the former sort either. There simply is no algorithm-- no systematic computation or step-by-step procedure, whatever our mental or mechanical resources, which will tell us in each case whether a finite cellular arrangement embedded in our infinite sea of yellow will or will not result in progressive conquest by green.
The final step of the proof is to show that the classical undecidability that holds for abstract machines, carried over to competitive automata, is ultimately an undecidability within game theory as well: the undecidability of the Spatialized Prisoner's Dilemma.
This is in fact the easiest step of all. What are required are simply specifications for a set of Prisoner's Dilemma strategies which will, in competition with each other, generate payoffs corresponding to the scores used in constructing the competitive cellular automata outlined above. Although somewhat tricky to construct, such a set of strategies easy to exhibit (see Appendix).
The core result, then, is that spatial arrays of Prisoner's Dilemma strategies will evolve in precisely the manner we've outlined for certain competitive automata. Arrays of Prisoner's Dilemma strategies will thus be capable of simulating the behavior of arbitrary abstract machines, and will inherit the undecidability we know to hold for those machines. By two transitional steps, then, classical undecidability will characterize the Spatialized Prisoner's Dilemma as well. Gödel is getting close.
Cooperative behavior is a basic fact of both economics and biology. Accounting for that fact is a theoretical challenge, and both theoretical economics and theoretical biology have imported resources from game theory in the attempt to do so. The primary model appealed to in both disciplines has been the Prisoner's Dilemma, which in iterated and spatialized forms offers a compelling picture of surprising but intelligible ways in which cooperation can arise from and serve the needs of self-interest. [4] These game-theoretic models thus constitute some of our simplest attempts at understanding this aspect of ourselves as both biological and social organisms.
Limitative results like that I've just sketched indicate how classical Gödelian undecidability shows up in even these simple models. In that sense it refuses to keep its intellectual distance, and refuses to stay safely locked away in the remote reaches of axiomatic arithmetic. [5] The phenomenon of undecidability, it turns out, characterizes even some of our simplest models of ourselves.
None of this, of course, should be taken as indicating that game-theoretic modelling is somehow conceptually doomed or hopeless, any more than standard Gödel results indicate that arithmetical programming is doomed or hopeless. None of it indicates that there is anything wrong with our attempts to use the Spatialized Prisoner's Dilemma as a model within either biology or economics. If anything, the work offers rather a reflection on the surprising depth of even the simple models we do now use: simple as they are, those models are deep enough to exhibit the classical phenomena of undecidability. Thus even if biological or economic phenomena were themselves as simple as our simplest existing models, they would exhibit a richness and complexity comparable to that of mathematics as a whole. We know of nothing conceptually richer.
1. For present purposes, building on work by Martin Nowak and Karl Sigmund, I will use the convenient mathematical fiction of infinitely iterated games (Nowak 1990, Nowak and Sigmund, 1989, 1992, 1993). Often it is easy to predict that strategies pitted against each other in an iterated game are bound to settle down into some monotonously repeated pattern of play. From their specifications, for example, we might be able to tell that a pair of Strategies S1 and S2 will establish and then simply repeat a pattern such as the following:
Strategy 1: DD CDCDCDCD CDCDCDCD CDCDCDCD ... Strategy 2: CD CDDCCCDC CDDCCCDC CDDCCCDC ...
The longer a finite iterated game we play, the more the relative scores in this repeated unit will matter and the less will matter any score differences before the period is established or in any fragmentary period played at the very end. Average scores within the repeated unit of play alone can thus be taken as a limit towards which average scores over finite games of increasing length will tend. What we take as the score of Strategy 1 vs. Strategy 2 in an infinitely iterated game is simply that limit. In this example scores of our two strategies over the repeated unit of play stack up as follow:
points: 31053505
Strategy 1: CDCDCDCD
Strategy 2: CDDCCCDC
points: 31503050
Strategy 1's average over the repeated period is 22/8 or 2.75.
This is the limit towards which its average score will converge in games of increasing length and what we take as its pure score in a game of infinite length. Strategy 2's score is 2.125. As noted, it is scores of this type for infinitely iterated games that are used throughout. Basic results will also hold, however, for finite games of sufficient length.
2. The question used to illustrate undecidability throughout the paper is whether a single strategy will dominate to conquest. It should be noted, however, that this is only an example. Given the basic method of proof other properties of arrays can be shown to be undecidable in precisely the same way: whether TFT will ever be completely extinguished in an array, for example, or whether good in the guise of a certain level of generosity will eventually triumph.
3. The or gate is ascetically simple and self-evident. The operation of the negation loop, however, is somewhat more complex. Here we assume a convention of spaces between signals sent along a wire; for purposes of illustration we've assumed 30 ticks between consecutive signals. The purpose of a negation inverter is to reverse a timed '1' signal to '0', or to replace a timed '0' with '1'. The lower loop of this negation structure does this by cycling around an electron which will 'kill' an electron coming from the left-- converting a '1' to a '0'-- or will simply move out to the right if there is no electron for it to kill at the proper time-- converting a '0' to a '1'. An incoming '1' therefore gives us a '0', an incoming '0' a '1', exactly as required.
4. Cooperative generosity emerges in spatialized models, in fact, even beyond what might be expected from iteration alone. See Nowak and May, 1992, and Grim, 1993.
5. The undecidability results outlined above do require an infinite field, and in that regard do retain an atmosphere of the abstract. The modelling of Minsky Register machines, for example, requires an infinite yellow sea in order to allow memory cores to expand as needed.
Were we to impose practical finite limits on arrays, formal undecidability would be avoided. But practical undecidability, in the form of unmanageable complexity, would remain. For finite arrays, given certain strategy assignments to n chosen cells, the question of whether a single strategy will prove triumphant appears to be exponential in n. If we cut the question further down to size, asking whether conquest will occur by a time limit which we carefully specify using some figure polynomial in n, our problem is still NP-complete. See Grim, 1994.
Axelrod, R., 1980a. "Effective Choice in the Prisoner's Dilemma," Journal of Conflict Resolution 24: 3-25.
Axelrod, R., 1980b. "More Effective Choice in the Prisoner's Dilemma," Journal of Conflict Resolution 24: 379-403.
Axelrod, R., 1984. The Evolution of Cooperation, New York: Basic Books.
Axelrod, R., and W. Hamilton, 1981. "The Evolution of Cooperation," Science 211: 1390-1396.
Berlekamp, E., Conway, J., and Guy, R., 1982. Winning Ways for your Mathematical Plays III, London: Academic Press.
Demongeot, J., Golés, E., and Tchuente, M., eds. 1985. Dynamical Systems and Cellular Automata, New York: Academic Press.
Dewdney, A., 1990. "The celllar automata programs that create wireworld, rugworld and other diversions," Computer Recreations, Scientific American 262: 1, 146-149.
Grim, P., 1993. "The Evolution of Greater Generosity in the Spatialized Prisoner's Dilemma," forthcoming in Biosystems.
Grim, P., 1994. "An NP-Complete Question Regarding the Spatialized Prisoner's Dilemma," research report #94-03, Group for Logic and Formal Semantics, Department of Philosophy, SUNY at Stony Brook.
Mar, G., and P. St. Denis, 1993. "Chaos and Cooperation: Two-Dimensional Prisoner's Dilemmas in Continuous-Valued Logic," International Journal of Bifurcation and Chaos, August 1994.
Nowak, M., 1990. "Stochastic Strategies in the Prisoner's Dilemma," Theoretical Population Biology 38: 93-112.
Nowack, M., and R. May, 1993. "The Spatial Dimensions of Evolution," International Journal of Bifurcation and Chaos 3: 35-78.
Nowack, M., and K. Sigmund, 1989. "Game-Dynamical Aspects of the Prisoner's Dilemma," Applied Mathematics and Computation 30: 191-213.
Nowack, M., and K. Sigmund, 1992. "Tit for tat in heterogeneous populations," Nature 355: 250-252.
Nowack, M., and K. Sigmund, 1993. "A strategy for win-stay, lose-shift that outperforms tit-for-tat in the Prisoner's Dilemma game," Nature 364: 56-58.
Silverman, B., 1987. The Phantom Fish Tank: An Ecology of Mind, Logo Computer Systems: Montreal.
Toffoli, T., and N. Margolus, 1987. Cellular Automata Machines: A New Environment for Modelling, Cambridge, MA: MIT Press.
Wolfram, S., 1984. "Cellular automata as models of complexity," Nature 311: 419-424.
Wolfram, S., 1986. Theory and Applications of Cellular Automata, Philadelphia: World Scientific.