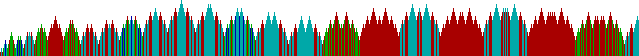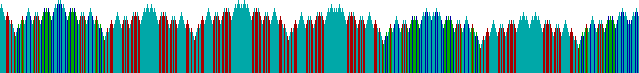 , which can be read as NOR. As is well known,
either NAND or NOR
suffices as a complete base for all Boolean connectives.
, which can be read as NOR. As is well known,
either NAND or NOR
suffices as a complete base for all Boolean connectives.'Rug' Enumeration images
We begin with an extremely simple formal system, for which we will
construct several different forms of images. The system at issue is
propositional logic, made even simpler by restricting it to a single
sentence letter p. In order to make things simpler still, we use a single
connective: either the Sheffer stroke | , which can be read as NAND, or the
dagger  , which can be read as NOR. As is well known,
either NAND or NOR
suffices as a complete base for all Boolean connectives.
, which can be read as NOR. As is well known,
either NAND or NOR
suffices as a complete base for all Boolean connectives.
Our goal, then, is to construct an image of truth-values for all formulae
expressible in terms only of p and | or  The values at
issue are merely
four, equivalent to p, ~p (p|p or p
The values at
issue are merely
four, equivalent to p, ~p (p|p or p  p) tautology
p) tautology  or contradiction
or contradiction  . In
Figures 4 through 8 we use the following colors for these values: green for p,
blue for ~p, red for tautologies and dark blue for contradictions.
. In
Figures 4 through 8 we use the following colors for these values: green for p,
blue for ~p, red for tautologies and dark blue for contradictions.
Let us start with a simple 'rug' pattern with an enumeration of all formulae expressible in terms of our single sentence-letter and single connective. For a first enumeration we represent the plan of the rug is laid out schematically as follows (Figure 3)2.

Here formula 1 is p p, formed by a single stroke between the formula heading its row and the formula at the top of its column. That formula, now simply labelled '1', is then placed in the second position along each axis. Formula 2 is formed as a 'slash product' of the formula heading its row and its column -- in the form (row column) -- in the same way. Formula 2 is thus (p|1) or (p|(p|p)). Formula 2 is added as the third formula on each axis. Formula 3 is ((p|p)|p), formula 4 is (p|(p|(p|p))), formula 5 is ((p|p)|(p|p)), formula 6 is ((p|(p|p))|p), and so forth. The pattern continues to generate progressively longer formulae, constituting in the abstract an infinite partial plane extending to the bottom and right and containing all formulae of our simple single- sentence-letter form of propositional calculus.
In Figure 4 the schema is shown in shades of color. Squares correspond
directly to the formulae indicated in the schematic sketch above, including
formulae along the axes, and are colored in terms of their values: as
noted, green = p or equivalent formulae, light blue = p|p or ~p, red
represents tautologies 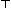 and dark blue represents
contradictions
and dark blue represents
contradictions 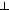 . The first
graph in Figure 4 is a smaller fragment of the upper left corner of the
rug, with the values of formulae indicated on axes as well. The second
image in Figure 4 shows a larger section, incorporating the first.
. The first
graph in Figure 4 is a smaller fragment of the upper left corner of the
rug, with the values of formulae indicated on axes as well. The second
image in Figure 4 shows a larger section, incorporating the first.

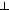 | x) and (x |
| x) and (x |
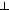 ) will be tautologous
for any x: once any formula on either axis has the value , any formula
composed from it with a single stroke will have the value . Closer
attention shows that rows in which the value of the formula at the top is
will simply reflect the value of the formulae on the column axis, with the
same true for columns with the value and the formulae listed along the top.
) will be tautologous
for any x: once any formula on either axis has the value , any formula
composed from it with a single stroke will have the value . Closer
attention shows that rows in which the value of the formula at the top is
will simply reflect the value of the formulae on the column axis, with the
same true for columns with the value and the formulae listed along the top.
 Fig. 5
Fig. 5
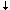 . Side by side, Figures 4 and 5 also serve to
make obvious
certain relationships between these two connectives: the fact that a
contradiction on either side of the stroke gives us a tautology, for
example, whereas a tautology on either side of the dagger gives us a
contradiction. It is clear that dagger tautologies mirror Sheffer stroke
contradictions, with dagger contradictions corresponding to Sheffer
tautologies. For simple systems with a single sentence letter, moreover,
the values of all contingent formulae in each system are the same. In none
of these cases do our images offer genuinely new information regarding the
stroke and dagger, of course--all the facts indicated are well known--
though these patterns do make such features vividly evident.
. Side by side, Figures 4 and 5 also serve to
make obvious
certain relationships between these two connectives: the fact that a
contradiction on either side of the stroke gives us a tautology, for
example, whereas a tautology on either side of the dagger gives us a
contradiction. It is clear that dagger tautologies mirror Sheffer stroke
contradictions, with dagger contradictions corresponding to Sheffer
tautologies. For simple systems with a single sentence letter, moreover,
the values of all contingent formulae in each system are the same. In none
of these cases do our images offer genuinely new information regarding the
stroke and dagger, of course--all the facts indicated are well known--
though these patterns do make such features vividly evident.
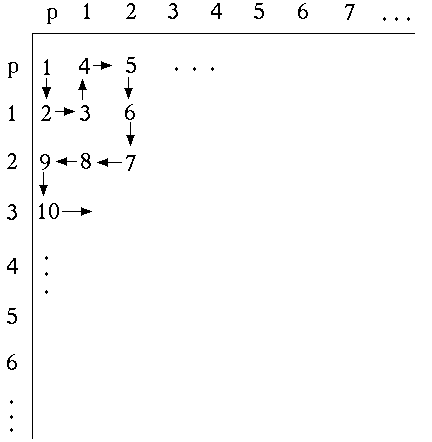
Fig. 6
Figures 7 and 8 show a rug pattern using a different enumeration of
formulae, following the alternative schematic in Figure 6.

Fig. 7 NAND using square enumeration

Fig. 8 NOR using square enumeration
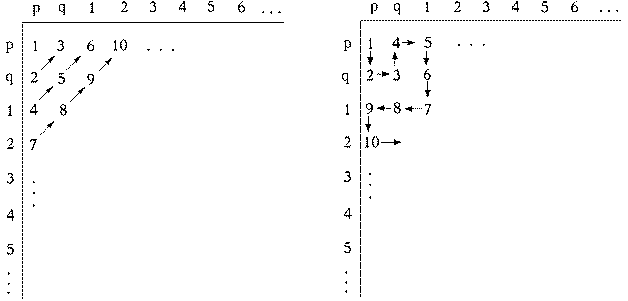

NAND NOR

Fig. 11


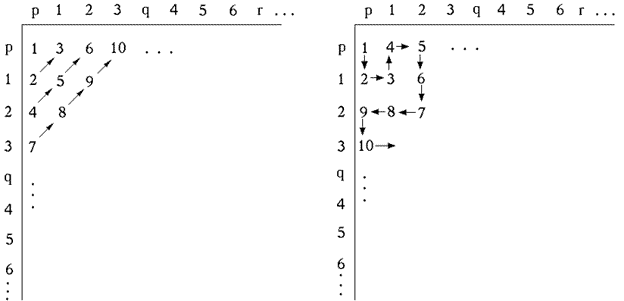 Fig. 14
Fig. 14
 x,
x,  y,
y,  z along just one axis.
Here the application of a lone quantifier to formulae in its row could be
interpreted as a universal quantification in that variable over that
formula. All other intersections would be interpreted as before, in terms
for example of the Sheffer stroke (Figure 15). Since existential
quantification can be expressed in terms of universal quantification and
negation, and the latter can be expressed by the Sheffer stroke in familiar
ways, such a schema will include all wffs of predicate calculus involving
only monadic predicate letters, together with all corresponding
propositional formulae. In assigning values to such a grid, a special
'formula value' would have to be reserved for mere propositional formulae,
representing the fact that they fall short of full formal sentences capable
of truth values.
z along just one axis.
Here the application of a lone quantifier to formulae in its row could be
interpreted as a universal quantification in that variable over that
formula. All other intersections would be interpreted as before, in terms
for example of the Sheffer stroke (Figure 15). Since existential
quantification can be expressed in terms of universal quantification and
negation, and the latter can be expressed by the Sheffer stroke in familiar
ways, such a schema will include all wffs of predicate calculus involving
only monadic predicate letters, together with all corresponding
propositional formulae. In assigning values to such a grid, a special
'formula value' would have to be reserved for mere propositional formulae,
representing the fact that they fall short of full formal sentences capable
of truth values.This illustration has been limited to monadic predicates simply because the scheme becomes so complicated so quickly even in that case. A representation of the full propositional calculus would demand only the further complication that we include all n-valued Predicate letters paired with n-tuplets of our variables. These can be generated in separate grids first so as to form a single enumeration, then introduced into the main grid in the position of P1, P2, P3... (Figure 15).

If we return for a moment to the simple form of propositional calculus with which we began, restricted to a single sentence letter, it should be clear that either of the enumerations offered above will generate progressively longer wffs. It is not true, of course, that the length of wffs within such an enumeration increases monotonically; formula 10 in our original enumeration is shorter than formula 9, for example. Along the diagonal of either schema, however, formulae do increase in size with each step.