Patrick Grim
Group for Logic and Formal Semantics
Philosophy
SUNY at Stony Brook
I was asked to outline a fuzzy logic approach to the sorites. What's good about this approach--what makes it a fairly happy face, in my view, is this. It starts with two simple claims about our language that I think just have to be right. On the basis of essentially those two claims alone it offers what I think is a very plausible account of both (1) what really is wrong with the argument and (2) why there doesn't seem to be anything wrong with the argument.
What makes it only a fairly happy face are difficulties that arise at a second level--at the level of trying to elaborate the basic claims about our language within a more complete and more formal semantics. Here there are some serious problems. I have some suggestions to make at that level, on which I'll want to hear your views. But for starters I just want to insist on this as a second level of inquiry. I think there is an intuitive fuzzy approach to the sorites that has a great deal of plausibility. But there are some difficulties in trying to formalize a fuzzy semantics adequate to that approach.
[Let me also emphasize that I am for the moment concerned only with offering a fuzzy treatment of the sorites. I'm not offering a fuzzy logic treatment of vagueness in general.
I am not offering a defense of all aspects of all types of fuzzy logic. Throughout I will be interested in developing the basic principles of fuzzy logics just so far as this solution to the sorites demands.]
I. Here is the fuzzy approach in its simplest terms. This is what I most like about the approach, and that for which all the rest is done.
We start with two simple facts about our language:
(1) First, that at least some of our terms apply as matters of degree. Whether someone is tall or short isn't like an on-off switch. It's a matter of degree: you can be very short, or fairly short, or more or less tall, or extremely tall. You start off very short, and in the natural course of things you grow: you get taller. Some people, in fact, grow up to be tall.
Tallness and baldness and redness and heapitude are, after all, continuous phenomena. How bald or tall you are is a matter of degree.
[A few minor asides:
For present purposes I don't think it matters whether you say that the properties themselves are matters of degree--that baldness comes in degrees--or that our terms apply as matters of degree. Those are complementary 'metaphysical' and 'linguistic' ways of presenting the approach.
I said I wouldn't attempt to offer a fuzzy approach to vagueness in general. All I want to offer, in fact, is a fuzzy approach to this: to continuous phenomena, or matters of degree. Other aspects or varieties of vagueness--context sensitivity, relativity to comparative class, and perhaps even some 'borderline' phenomena--I merely put to the side.
The claim is that some of our terms apply as matters of degree. That leaves it open whether some don't, or whether all do. It also leaves it open whether, if some do and some don't, there are terms in natural language that are ambiguous between the two. ]
So the first simple claim about our language is simply that there are continuous phenomena, for which we have terms which apply as matters of degree.
(2) The second claim about our language is one of pragmatics. For general purposes of communication, we quite generally let people get by with claims that are perhaps less than perfect. We have learned to tolerate a range of grammatical errors and mispeakings without flinching.
To do otherwise would generally obstruct rather than facilitate communication. We also tolerate at least small measures of inaccuracy.
[If the weather man's prediction is that the temperature will be 70, when in fact the high is 69, we congratulate him on his accuracy. We don't accuse him of lying to us. If a friend says he'll meet us for lunch at noon, and he's there at 12:01, we don't get all huffy and accuse him of false utterance. For all practical purposes, what he said was right on the money. "True enough."]
Those are the two basic claims on which the fuzzy approach is built. What I want to emphasize to begin with is just how plausible those two claims are. We have terms which do apply as matters of degree. Indeed, I think, for the purposes our language serves, we must. And the pragmatics of our language are such that we do tolerate small measures of inaccuracy. Indeed, I think, for the purposes our language serves, we must.
II. The sorites argument can of course be formulated in a number of ways. One way is as a set of apparently innocuous propositions that turn out to be inconsistent. This is of course the Peter Unger form:
1. There is at least one swizzle stick.
2. If anything is a swizzle stick, it consists of some finite number of atoms, but more than
one.
3. If anything is a swizzle stick, and you remove a single atom, you still have a swizzle
stick.
Another formulation is that which takes us from an obvious truth to an obvious falsehood.
The obvious truth is perhaps that Yul Brynner is bald before his hair transplant operation. The obvious falsehood is that he's still bald after his (successful) hair transplant operation.
We suppose a transplant operation that proceeds in 20,000 steps, each involving the addition of a single hair. The sorites reasoning takes us from:
1. Yul Brynner before his transplant operation has 0 hairs.
2. Yul Brynner before his transplant operation is bald
3. If someone with n hairs is bald, that someone with n+1 hairs is still bald
to
4. Yul Brynner after his transplant operation is bald.
[It is also clear, of course, how one could convert any contradiction form of the argument to a false conclusion form and vice versa.]
Both of these, however, are offered in a condensed form. When you try to show people how the Unger argument leads to inconsistency, you give a more complete form, which goes something like this:
1. If anything is a swizzle stick, it consists of a finite number of atoms, but more than
one.
2. Here I have a swizzle stick.
3. Now if I remove a single atom from any swizzle stick, I'll still have a swizzle stick.
[remove one]
4. So I still have a swizzle stick.
5. Now if I remove a single atom from any swizzle stick, I'll still have a swizzle stick.
[remove one]
6. So I still have a swizzle stick.
7. Now if I remove a single atom....
You construct a chain, in other words, using repeated instantiations of your inductive premise.
In the Yul Brynner case, when you try to show people how the argument leads from obvious truths to obvious falsehoods, you step them through the first steps of a similarly expanded form:
[starters:]
1. Yul Brynner before his transplant operation has 0 hairs.
2. Yul Brynner before his transplant operation is bald.
[general principles:]
3. If someone with n hairs is bald, that someone with n+1 hairs is still bald.
4. At step m of the transplant operation, we add a single hair (for m=1 to 20000)
[the series:]
5. At step 1 of the transplant operation, we add a single hair. (4, UI)
6. If someone with 0 hairs is bald, that someone with 1 hair is still bald. (3, UI)
7. After step 1 of the transplant operation, Yul Brynner has 1 hair. (1, 5, arithmetic)
8. After step 1 of the transplant operation, Yul Brynner is still bald. (6,1,2,7, MP)
9. At step 2 of the transplant operation, we add a single hair. (4, UI)
10. If someone with 1 hairs is bald, that someone with 2 hairs is still bald. (3, UI)
11. After step 2 of the transplant operation, Yul Brynner has 2 hairs. (7, 9, arithmetic)
12. After step 2 of the transplant operation, Yul Brynner is still bald. (10, 7, 8, 11,
MP)
13. At step 3 of the transplant operation, we add a single hair. (4, UI)
14. If someone with 2 hairs is bald, that someone with 3 hairs is still bald. (3, UI)
15. After step 3 of the transplant operation, Yul Brynner has 3 hairs. (11, 13,
arithmetic)
16. After step 3 of the transplant operation, Yul Brynner is still bald. (14, 11, 12, 15,
MP)
...
80004. After step 2000 of the transplant operation, Yul Brynner is still bald
[The generalization of the inductive step and its instantiations are in bold because they are the key to the fuzzy solution.]
So what's wrong with the argument? It appears to move, by unexceptionable logic, from undeniable premises to an unacceptable conclusion. What's the problem?
The fuzzy happy face solution is this:
* The central terms at issue ('bald', for example, or 'is a swizzle stick') apply as a matter of degree.
* In expanded form, the argument depends on a bunch of conditionals written in terms of those degree terms, of the form, for example, of step 14:
14. If someone with 2 hairs is bald, that someone with 3 hairs is still bald:
or
If this is a swizzle stick, and I remove an atom like this [flick], I still have a swizzle stick.
* Those conditionals are very close to right. In general, a conditional (p q) which moves from something p that holds to a certain degree to something q that holds to a just slightly lesser degree is a conditional which loses just a very small bit in the transition. A conditional which loses next to nothing in the transition is a very respectable conditional.
* Such a conditional is in fact so respectable, given our pragmatics, that we'd almost always treat it as simply true.
That's why everything looks okay with the sorites: our starting premises are all true, and the conditionals we use at each step are very close to true--so close as to be treated pragmatically as 'true' for all practical purposes.
The reason everything isn't okay with the sorites is that these aren't practical purposes. These are theoretical purposes. We envisage an incredible chain of applications of nearly true conditionals, and in that theoretical construction the inaccuracies--so slight each time as to make each conditional appear unexceptionable--add up.
At each step we have a little less of a swizzle stick, and at each step Yul is a little less bald. The conditional used each time (if we had a swizzle stick, we still have one...If Yul was bald, he still is) loses so little from antecedent to consequent as to be treated as true in each single case. But in an extended chain the little bits add up. In the end we will have gone by many tiny steps (each covered by a conditional which leaks only a little bit) from a swizzle stick to nothing. In the end we've gone from a bald man to a man who isn't bald any more.
III. Okay. That's the intuitive core of the fuzzy approach. I think it takes us from some simple claims about our language--claims that just have to be true--to a very plausible account of both why the sorites argument looks okay and why the chain of argument takes us from apparent truth to clear falsehood. I think that intuitive core is very attractive.
What I want to do is to turn to level two, elaborating on that intuitive core.
The name of the game at this level is to sketch more completely a semantics for degree terms that will do justice to this intuitive strategy regarding the sorites. I separate it as a second level, of course, because I want to localize failure. The fact that a particular attempt at a richer semantics fails may impugn only that particular attempt: it may mean we haven't yet succeeded at an adequate fuzzy semantics, not that the basic fuzzy solution for the sorites is not still fundamentally sound.
What I want to do at this point is to sketch some minimal semantic models. These are 'minimal' in the sense that I will insist only that they give us the basic principles used in the intuitive solution. I won't, for present purposes, feel any need to develop them beyond that.
A. At this stage, however, we face a fundamental problem.
What we're looking for is a model of a certain aspect of vagueness: a model of matters of degree. But one thing that is clear about the terms at issue--baldness, redness, swizzle-stick-itude--is that although they apply as matters of degree, they don't apply in terms of precise degrees. You can be very very bald, but you are not a precise degree bald. You can be very very short, but you aren't a precise degree short.
[In fact, if you ask 'Precisely how tall is he?', the answer you get isn't 'he's precisely .98 tall' but 'he's precisely 6'2" tall'--you get a measurement in feet and inches rather than a precise degree of tallness. If you say, 'yes, but precisely how tall is 6/2?' you're asking for the wrong thing. If you ask 'precisely how old is he?', you don't get 'precisely .76 old' but '56 years old'. And if you ask, 'Yes, but precisely how beautiful is she?', you don't get any answer at all.]
The terms we're dealing with apply as matters of degree, but as not as matters of precise degree. I think that is probably just another name for the phenomenon of 'higher-order vagueness'. I think the plausibility of our conditionals in the sorites rests on precisely that same phenomenon. But that poses a problem. When we ask for a formal semantics we're standardly asking for a specification of a set of models, in each of which a set of atomic sentences is assigned a particular valuation and in which molecular sentences are then assigned values recursively. Classically, the values assigned are simply 'true' or 'false'. Not-so-classically, the whole attempt at a formal semantics seems to demand that at least some specific values are assigned.
The problem is that asking for that kind of semantics seems diametrically opposed to the phenomena of imprecise matters of degree. Any semantics which assigned sentences involving these terms precise values would seem guaranteed to go wrong. Construct any precise semantics for these sentences and your semantics will be wrong.
So what do we do? We loosen our requirements. For this class of terms we want a semantics which doesn't supply precise values: which supplies only imprecise values.
How do we do that? Well, I have a few ideas. I'm going to sketch four possible directions, though often very cursorily.
Let me also offer another take on these four fuzzy semantics. The standard semantics offered for fuzzy logic is in terms of precise numerical values. Quite frankly, that seems to be where it gets into trouble. Each of these can thus be seen as an attempt to do fuzzy semantics either without the numbers, or with the numbers muffled in such a way that those standard problems are avoided.
These are often very different approaches. What will be particularly interesting will thus be to see if any of them work better than the others.
A. One semantic approach would be to build into our symbolism a phenomenon that is itself a matter of imprecise degree. Suppose we assign statements not a 'T' or an 'F', not a '1' or a '0',
but a shade of pencilled grey. Almost black for truth, almost white for falsehood, with lots of shades in between.
What would a 'shady semantics' look like? We envisage atomic sentences assigned pencilled
shades as their values. At step 100 of the transplant operation, for example, 'Yul is bald' might be assigned this value:
Yul is bald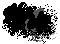 
(very dark)
At step 10,000 'Yul is bald' might be assigned this value instead:
Yul is bald 
(much lighter)
In a shady semantics, those pencilled shades are our assigned values. Sometimes, of course, you wouldn't be sure whether something was fully true, nor could you always be sure whether two sentences had the same value or not. That's precisely the point. Welcome to imprecise semantics.
On that basis, our combinatorial rules might look like the following.
Given a shade for p, the shade appropriate for ~p is the complementary grey: as white as p's shade is black, as black as p's shade is white.
Given shades for p and q, the shade for p & q is whichever is lighter.
Given shades for p and q, the shade for p v q is whichever is darker.
Those are interesting, but (with the partial exception of conjunction) aren't in fact crucial to the solution to the sorites for which we are trying to supply a semantics. All we really need is this:
Given shades for p and q, the shade for p -> q is:
if the shade for q is darker
than p, otherwise lighter than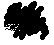 
to the
extent that p is darker than q .
A conditional in which the consequent has a shade only slightly lighter than the antecedent, then, will be shaded very dark. That's just what we need for the fuzzy account. Each of our conditionals in the sorites chain will be shaded almost black, as will our starting points. The shading for 'Yul is bald' will decrease at each step of the argument, however, leaving us with a virtually white shading at the end: a portrait of what seems right about the sorites, and what goes wrong, in semantic shades of grey.
B. Here is a second approach--I'll call it a 'very very' semantics. On this approach, the semantics we need would be a branch of a yet-to-be-developed general semantics for comparatives.
For the kinds of terms at issue we can quite generally construct a scale of imprecise degree categories. To these, in fairly obvious ways, will correspond imprecise partial truth-values:
... ...
very very very bald 'Bill is bald' very very very true
very very bald very very true
very bald very true
sort of bald sort of true
somewhere in the middle somewhere in the middle
sort of unbald sort of untrue
very unbald very untrue
very very unbald very very untrue
very very very unbald very very very untrue
... ...
[often these are more easily construed in terms of pairs of opposing terms--'bald' on one end and 'hairy' on the other, for example--but that's a complication I've put aside here.]
We take those values on the right side as the basic values of our semantics: a countable set of imprecise partial truth values.
Here I issue a promissory note for future connective rules. Most of those will come with the development of a logic for comparatives. But we can at least sketch a few basic principles.
A logic for comparatives can be expected to include treatment for 'is as bald as', 'is balder than...' and perhaps even 'is a little balder than...'. Among the principles we would expect to hold for any acceptable model will be things like these. Where D is any of our left-hand categories (like 'fairly bald'):
If Bill is as bald as Mike, and Bill is D, then Mike is D.
If Bill is balder than Mike, and Mike is D, then Bill is at least D.
Since our right-hand truth-categories correspond to our left, similar principles will hold for truth.
What is most crucial for our purposes is that the following principles, governing a certain class of conditionals, would also seem very plausible:
Where Bill is just a little balder than Mike,
'If Mike is bald, then Bill is bald' will qualify as fully true
and
'If Bill is bald, then Mike is bald' will qualify as very true but not fully true.
The second is the 'very very' semantics treatment of the conditional that we need for the intuitive solution.
C. In my book both of these qualify as fuzzy semantics, though neither use numerical truth-values. Indeed that is part of the point: the basic trick of the fuzzy solution to the sorites doesn't depend on the numbers. If a fuzzy semantics written in terms of numbers causes problems, look for a fuzzy semantics without them.
The other two semantics I want to outline do use numbers, though both try to muffle them in certain ways.
Here the first proposal is a rough semantics. The semantics assigns numerical truth-values to propositions, but on the understanding throughout that all numerical assignments are only rough assignments.
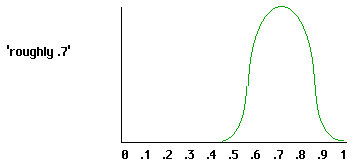
We can introduce it like this. Consider a term that applies as a matter of degree--'old', say, or 'young'--but that is conveniently correlated with a measure such as years of age. And consider constructing a chart like the following. On the x-axis we have age in years. On the y-axis we want to graph the rough degree to which the term 'old' applies:
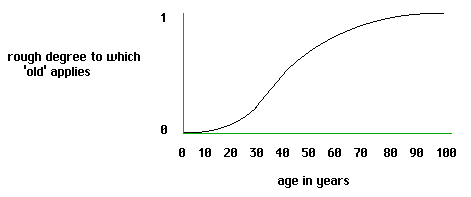
Once we envisage modeling (rough) degrees of predicate application in this way, it seems natural to make truth follow the same pattern. If 'old' applies to Grim roughly to degree .8, 'Grim is old' can be thought of as true to degree .8. Quite generally, we employ a generalization of the Tarski schema
[x is P] is true to degree d <-> x is P to degree d
Here it is important, however, to keep our semantics conceptually separate from our original language. What we asked our semantics to do was to assign rough numerical values for our sentences. That doesn't mean that those value attributions become part of our original language. In our semantics we may apply 'old' to Grim to roughly degree .8. But that doesn't mean that
either 'roughly .8 old' or 'roughly .8 true' are predicates of our original language. They are merely convenient devices within our semantics.
At this point, then, the big philosophical commitments are these: that terms apply as matters of degree, and that we can offer models of those matters of degree in terms of rough values in the [0,1] interval. Our model will operate in terms of rough degrees of truth that follow rough degrees of predicate application.
Once we have that, we can fill out rules for the standard connectives as follows. Where /p/ indicates the (rough) value of p,
/~p/ = 1- /p/
/p v q/ = max[/p/, /q/]
/p & q/ = min[/p/,/q/]
These are direct generalizations from the classical case. They are not the only possible generalizations--once you go to an interval of values from merely T,F or 1,0 there are always alternative generalizations, but there are some formal constraints which make it clear that these are at least non-arbitrary.
[In particular, for max and min:
If conjunction and disjunction are:
1. Functions strictly of the values of their components. [prob. violates]
2. Commutative, associative, and mutually distributive
3. Continuous and non-decreasing with respect to each input
4. p & p and p v p are strictly increasing.
5. Conjunction is less than or equal to min, and disjunction is less than or equal to
max
[probability violates the second]
6. Conjunction of 1 and 1 = 1 and disjunction of 0 and 0 = 0
Then we are forced to max and min.]
What of the conditional? Here too there are options. That which seems to be preferred throughout the literature, however, is the Lukasiewicz conditional:
/p -> q/ = min[1, 1-/p/ + /q/]
or equivalently
/p -> q/ = 1 if /p/ < /q/, 1-abs[/p/-/q/] otherwise
A conditional which preserves or gains truth from antecedent to consequent counts as fully true.
A conditional is false to the extent that it 'leaks' truth from the antecedent to the consequent.
[A prime virtue of the Lukasiewicz conditional is that p p has a value of 1 whatever the
value of p. It also generalizes to a very nice biconditional:
/p <-> q/ = 1-abs[/p/-/q/]
A classical biconditional is false if the two differ in value. A Lukasiewicz biconditional is
false to the extent the two differ in value.]
Essential to this semantics, as I have outlined it here, is the idea that it is only rough numerical values that are applied. What precisely does that mean?
Here there are two approaches, I think. One is to stonewall--to treat 'rough' as a primitive: something in terms of which the semantics is written, but which has to be understood already. If we are going to give an imprecise semantics of any sort, the imprecision has to be built in somehow. In shady semantics, it is built in in terms of the inherent degree character of shading. In fuzzy language semantics, it is built in in terms of the vagueness of the 'very very's. In rough numerical semantics it is built in in terms of the imprecision of a primitive qualifier 'rough'.
There is also another possible approach to 'rough', though I'm less sure of this. Our semantics as outlined offers an assignment of values like 'roughly .8 old', 'roughly .7 true', and the like. If you want to know what 'roughly' means in those attributions, you're asking for a further semantics for 'rough'. 'Rough' is an imprecise degree term, of course, for which we can only give a rough semantics. But we might propose that the rough semantics for 'roughly .7 true', for example, might look something like this:
This is, I think, much in the spirit of Hartry Field's proposal in our first session, though it's written in terms of a loop rather than an infinite hierarchy. All of our semantics are rough semantics. If you want to know what 'rough' means in any context we can give you a similarly rough semantics.
D. The final approach I have to offer is a sketch for a fuzzy supervaluationist semantics.
Here again our semantics is in terms of numbers--.99 bald, .99 true, etc. Here as before it is crucial to emphasize that these numerical ascriptions are terms of art within our semantics alone, rather than part of our original language.
In a classical semantics, we have a set of acceptable models, or valuations, each of which assigns a value of 1 or 0 (true or false) to each of our atomic sentences. In fuzzy supervaluationalism we envisage a set of acceptable models, or valuations, each of which assigns some real value between 0 and 1 to our atomic sentences.
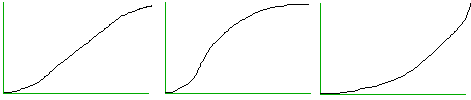
There may be various equally reasonable ways to make such an assignment. Each of the graphs shown, for example, may offer a respectable assignment for 'old' in terms of years of age. Not all ways are as reasonable, of course, and some are downright unreasonable. One of the strengths of this approach, however, is that it recognizes that quite different numerical assignments can be equally reasonable, and indeed incorporates those reasonable alternatives as its models.
Alternative reasonable valuations (distinct models) for old':
We can let our connectives in any world follow the pattern outlined in our rough semantics. The Supervaluationist component is this: that our logical principles will be those stateable in our original language which will hold in all such reasonable assignments, or in all admissible models. Perhaps we might also add a scale: something will qualify as a logical principle to the extent that it holds in all reasonable assignments.
Crucial for the fuzzy approach to the sorites, of course, is that this will be very true in all such models:
'If Bill is bald, and we remove a hair, then Bill is still bald'
[But note that the usual supervenient tautologies don't hold: 'p v ~p' is not fully true in all fuzzy models for p [indeed can take a value as low as .5], and thus won't be among our logical principles.]
Consider also the standard problem of 'higher-order vagueness' for classical supervaluationalism: the fact that a supervaluationist account seems to commit us to:
'There is an x such that Mike has x hairs and is bald, but Mike with x-1 hairs is not bald'
Unlike the classical case, in fuzzy supervaluationism this will be very untrue in all models. Using 'min' for conjunction ("but"), the best any instance of this could be is less than half true.
[What of: 'There is a point, or some magic number of hairs, at which you go from 1.0 bald to .9999 bald.'? We said that our logical principles were those expressible in our original language that held in all models. '1.0 bald' and '.9999 bald' are not expressions of our original language.]
V. Let me finally add some notes regarding semantic entailment. I'll do this in the terms of our 'rough' semantics, but it will be clear how it would apply to the others as well:
Classically, L double turnstile p applies if in no admissible model is every element of L true and p false. An argument is valid if in no admissible model are all premises true and the conclusion false.
For fuzzy models [still limiting arguments to finite premises] we might say: an argument is valid if in no admissible model is the value of the conclusion less than the value of the least premise.
Alternatively, and much in the spirit of a fuzzy approach, we might propose a variable notion of validity. A valid argument will be fully truth-preserving in all models. An invalid argument is one that will leak truth somewhere--and it is as invalid as its leak.
An argument will be valid to the degree that it preserves truth universally. It will be invalid to the degree that it leaks truth in the 'worst' model. We can take the variable measure of validity as one minus the measure of invalidity, so an argument will be valid to 1 minus the extent that the value of its conclusion is less than the value of its least premise in the model in which that measure is the greatest.
With that account of semantic consequence our analysis of the sorites will look like this.
Take Yul at any step in the proceedings. If 'bald' applies as a matter of degree, any of our semantics will supply a value for the extent to which 'bald' applies to Yul at that point. [Where they differ, of course, is in what kind of value is supplied--a penciled shade, a linguistic category, a rough number or the like.] Consistent with all approaches will be an assumption that degree to which 'bald' applies will decline in small amounts with the progressive addition of hairs. Yul becomes less bald with each additional hair. That seems precisely right to me.
Values for 'truth' can follow values for degree of predicate application in any of our semantics. Roughly put: with each additional hair it becomes less true that Yul is bald. [That seems harmless to me. I actually think we can do the whole trick without 'true', but never mind...]
What about the crucial instantiations of our inductive premise, like:
If someone with 200 hairs is bald, that someone with 201 hairs is still bald ?
Each such instance is a conditional from a case in which 'bald' applies to a certain degree to a case in which it applies to a very slightly lesser degree. Any of our semantics will give a very high value to such a conditional. Roughly put: all such conditionals are very very true.
What of the general inductive premise?:
If someone with n hairs is bald, that someone with n+1 hairs is still bald ?
If quantification corresponds standardly to conjunction, and given a semantics for conjunction in terms of 'min', our general inductive premise will be as true as its least true instantiation. It too will thus be very very true.
So are all the premises of our sorites true? Very much so, though not without qualification: the inductive premise in particular is merely very true.
Is the argument valid? In the first sense outlined, such that a valid argument is one such that the conclusion cannot be less true than any of its premises, it's clear that the full sorites argument is invalid. The value of our conclusion ('Yul is still bald') is less than that of any of the starter premises.
On this account, in fact, the individual steps of our argument will quite standardly be invalid: we will go from a partial truth (via something very very true) to something slightly less true. An invalid argument composed of invalid steps.
In the variable sense of validity outlined, validity is a matter of how much is lost. On this account, interestingly enough, each little step of the argument can still be 'very valid', because so little is lost. Nonetheless the chain as a whole gives us an argument that is very invalid. Variable validity thus has the following interesting feature: that an argument which uses a premise once may be more valid than one which uses that same premise multiple times. I've been told that Paul Ziff once claimed that sorites arguments were alright as long as you didn't use them too often.
So the sorites is, after all, both invalid and unsound. Why does it look so good? Because its premises are so very close to true and its individual steps are so very close to valid. Each step leaks just a little truth--so little that for practical purposes, for individual steps, we'd normally ignore it. But in a extensive theoretical series those leaks can add up. That's what's happening here.
VI. That's the basic strategy, outlined in four semantic variations. Let me also turn to some standard objections.
The primary objection to fuzzy logic as a treatment of vagueness is undoubtedly that (a) that it introduces a false precision, and thus (b) is unable to handle second-order vagueness--forcing us to presume, for example, that there is some exact point at which someone stops being young to degree 1 and becomes young to some lesser degree.
[Now let me repeat that what I've offered here is not intended as a fuzzy treatment of all vagueness--only of the matters of degree I think are crucial to the sorites. For present purposes, in fact, I've tried only to outline as much of a fuzzy semantics as is necessary for the basic fuzzy solution to the sorites. Nonetheless...]
Each of the semantic outlines is intended to address this in one way or the other.
A. The embarrassing question for shady semantics would be something like this:
A. Is there some magic point at which by the addition of a single hair the value of 'Yul is bald'
goes from 
to 
?
So what's the answer? Well, if you make those two shades clearly distinguishable, the answer is going to be 'no'. There is no such point, because the addition of a single hair never takes us so far.
In order for this to be plausible, the shades will have to be at least very close to indistinguishable.
But every point at which someone is
(this shade) bald is a point at which someone with 1 more hair is (indistinguishable shade difference) this bald. And of course that holds for
every shade.
If you tell me that this shade is just very slightly less than this shade, and then ask the question, the answer will be 'yes', regardless of that shade. That just means that addition of a single hair will make someone a very little bit less bald. That's what this is all about.
One way of making the point is this: we won't have embarrassing magic discontinuities in value assignment because our symbolism is itself explicitly written using a continuous phenomenon without magic break points.
B. For 'very very' semantics the embarrassing question would be something like this:
B. Is there some magic point at which by the addition of a single hair the value of 'Yul is bald' goes from 'very very true' to just 'very true'?
Here, I think, the answer is 'no'--or at least that we don't have to say so. 'Very very true' simply follows 'very very bald' in this semantics, and we no more need to say this than we need to say that a single hair marks the transition from 'very very bald' to 'very bald'.
C. The 'rough' and supervaluationist semantics outlined, of course, do work in terms of numbers at some level, and thus might seem more vulnerable to charges of false precision. Both try to muffle the numbers, though in different ways.
For rough semantics, the embarrassing question would be something like this:
C. Is there some magic point at which by the addition of a single hair the value of 'Yul is bald' goes from roughly 1.0 to roughly .999?
If the semantics works the way I want it to, the answer will be 'no'. If you understand what 'roughly' means, you'll know that roughly 1.0 is roughly .9999.
That is in line with the approach in which 'roughly' is taken as a primitive vague qualifier. I'd want the iterated 'roughly' to work the same way, but I'm not yet sure whether it does or not.
D. Finally, fuzzy supervaluationism. We've said that in all models this will be very untrue:
There an x such that: There is an x such that Mike has x hairs and is bald, but Mike with x-1 hairs is not bald
But what of attempts to phrase the embarrassing question like this?
D. Is there some magic point at which by the addition of a single hair the value of 'Yul is bald' goes from 1.0 true to .9999 true?
Each of our semantic models does assign values like '1.0 bald' and '.999'. But we've said those are just terms of art in the semantics: just some tools the stage hands use. The logical principles to which our semantics commits us, as outlined, are those expressible in our original language that hold in all models. This isn't one of them, because '1.0 bald' and '.9999 bald' are not expressions of our original language.
One might try to resurrect the problem with something like:
'Is there some magic point at which you go from fully bald to something less than fully bald?'
The answer to that depends on whether your original language has 'fully bald' in it. I tend to think that there is no such thing as 'fully bald' in ordinary English, unless we choose to specify it as meaning 'with absolutely no hairs'. If that is how we specify it, then, the answer is yes: with the addition of a single hair you will have made the transition from having absolutely no hairs to something a little less bald. But that doesn't seem very embarrassing.
Patrick Grim
Group for Logic & Formal Semantics
Philosophy
SUNY at Stony Brook
pgrim@ccmail.sunysb.edu