Evolution of Communication in Perfect and Imperfect Worlds

Patrick Grim, Trina Kokalis, Ali Tafti, and Nicholas Kilb

from World Futures: The Journal of General Evolution 56 (2000), 179-197

Group for Logic & Formal Semantics
Dept. of Philosophy, SUNY at Stony Brook

Abstract: We extend previous work on cooperation to some related questions regarding the evolution of simple forms of communication. The evolution of cooperation within the iterated Prisoner's Dilemma has been shown to follow different patterns, with significantly different outcomes, depending on whether the features of the model are classically perfect or stochastically imperfect (Axelrod 1980a, 1980b, 1984, 1985; Axelrod and Hamilton, 1981; Nowak and Sigmund, 1990, 1992; Sigmund 1993). Our results here show that the same holds for communication. Within a simple model, the evolution of communication seems to require a stochastically imperfect world.

Keywords: communication, computer modeling, stochastic, imperfection, evolution, cooperation

1. Introduction

Meaning has long been at the core of philosophical investigation. The classical philosophical tools for approaching meaning, however, have been introspection and linguistic intuition. In a tempting caricature of such an approach, one intuits what meaning is by rolling one's eyes into one's head and looking inwardly.

We are not alone in thinking that this is precisely the wrong approach.⁽¹⁾ A helpful analogy, perhaps, is the history of our understanding of biological life. Life remained a mystery as long as we tried to understand it as a simple something possessed by an individual at a particular time-an attempt to understand life that characterizes Mary Shelley's Frankenstein, for example. Contemporary understanding, in contrast, treats life as a complex continuum of properties that characterize a community of organisms evolving over time. Our conviction here, and the underlying philosophical motivation for the model we want to present, is that the same may be true of meaning: that the proper way to understand meaning may be not as an inner possession of an individual at a time but as a complex continuum of properties characteristic of a community-a community of communicators-evolving over time.

In what follows we outline a simple computer model for the evolution of communication. We are interested in particular in the circumstances under which strategies of communication will be selected for and can spread within a community. The particular finding we emphasize here is the importance of a stochastically imperfect world for that evolution: within the model outlined, it is only in an imperfect world that a strategy of communication proves successful.

2. Imperfection and Cooperation in the Prisoner's Dilemma

What we want to explore below is a simple model for communication. It is important to note a number of ways, however, in which that model builds on earlier work regarding cooperation.

For the last twenty years or so, the formal tool of choice for investigating cooperation and competition has been the Prisoner's Dilemma. In classical form, each of two players in the Prisoner's Dilemma has the option of cooperating with her opponent or defecting against her, with points awarded as follows:

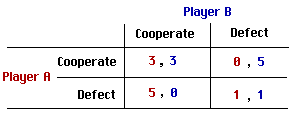
Here a payoff 5,0 indicates that 5 points go to player A and that 0 points go to player B. A payoff 0,5 indicates 0 points for A and 5 points for B.

Given this pattern of payoffs, it is clear that defection is the 'dominant' choice in a one-shot game: whichever choice the opponent makes, a player will gain more points by defecting than by cooperating. It is also clear, however, that if both players follow such a strategy everyone will do significantly worse than if both choose to cooperate.

The iterated Prisoner's Dilemma consists of a series of such games. Here the situation is more interesting, and strategies for continued play emerge: a strategy of cooperating in all cases (AllC), of defecting in all cases (AllD), or of responding to the opponent's previous play in kind. This last is the cooperative strategy of Tit for Tat (TFT), which responds to defection on the other side with defection but rewards a cooperative move with reciprocal cooperation.

The classic work on the success of TFT in the iterated Prisoner's Dilemma is that of Robert Axelrod. In two tournaments based on an open call for strategies, TFT emerged as the winner in round-robin competition of each strategy against all others (Axelrod 1980a, 1980b, 1984, 1985).⁽²⁾ TFT also displaced all competing strategies in a more sophisticated model in which strategies reproduce on each round in proportion to their success (Axelrod and Hamilton, 1981).

Axelrod's models, however, demand 'perfect' worlds of cooperation and defection. There is never any doubt about whether an opponent is cooperating or defecting on a particular round, and given a particular pattern of play all strategies specify full and faultless cooperation or defection on any round.

More recent work by Martin Nowak and Karl Sigmund, in contrast, models a stochastically imperfect world in which cooperation or defection is specified only in terms of some imperfect degree of probability (Nowak and Sigmund 1990, 1992; Sigmund 1993). The attempt is to add a measure of realism: here information may be imperfect regarding an opponent's play or a strategy may be able to execute a response only with a 'shaking hand'. The world of Nowak and Sigmund's models is thus an imperfect world of ubiquitous and inevitable stochastic noise. In such a model TFT, for example, appears only in a slightly imperfect guise: here TFT responds with cooperation to an opponent's cooperation with a probability of 0.99, rather than 1. In this imperfect world TFT similarly responds with defection to an opponent's defection with a probability of 0.99. Using c to represent a strategy's probability of cooperating in the face of cooperation, and d to represent a strategy's probability of cooperating in the face of defection, we can think of strategies in Nowak and Sigmund's imperfect world as pairs <c,d>.⁽³⁾ TFT thus appears in an imperfect world as <0.99, 0.01>.

The surprise is that in this imperfect world, with a model in other respects like Axelrod and Hamilton's (1981), it is not TFT that proves the final victor. Using a sampling of 121 strategies, imperfect Tit for Tat <0.99, 0.01> does dominate the population early in the game. TFT is then supplanted, however, by a strategy <0.99, 0.1> which returns cooperation with cooperation at probability 0.99 but forgives defection with a probability of 0.1 rather than merely .01. This more generous strategy is in turn replaced by a still more generous version <0.99, 0.2> which forgives defection with a probability of 0.2, and finally in the course of 12,000 generations by a version which forgives defection with a probability of 0.3. The ideal strategy for an imperfect world, in fact, is a 'Generous Tit for Tat' <1-, 1/3>, returning cooperation for cooperation at a rate infinitesimally close to 1 but responding generously to defection with cooperation at a rate of 1/3.

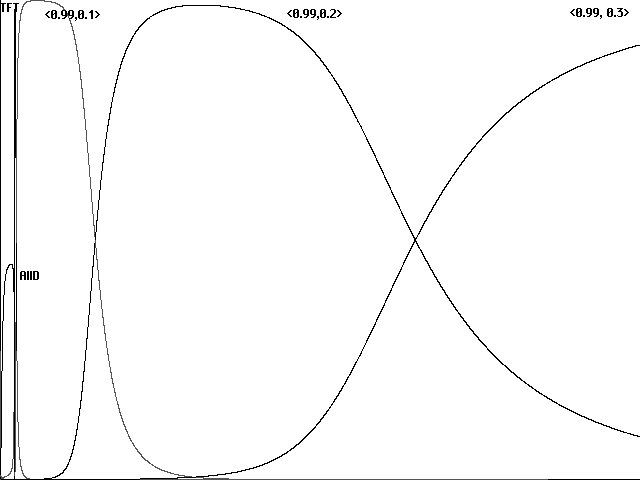
Fig. 1 Evolution of cooperation in an imperfect world (Nowak and Sigmund). Population proportions for labeled strategies shown over 12,000 generations for an initial pool of 121 stochastic strategies <c,d> at 0.1 intervals, full value of 0 and 1 replaced with 0.01 and 0.99.

In previous work, we have extended Nowak and Sigmund's attempt at realism by using a model that is spatial as well as stochastic. In a spatialized model, individuals are envisaged as cells in a cellular automata array. Cooperation and competition take place only locally-each cell plays an iterated Prisoner's Dilemma with only its eight immediate neighbors. Strategy change occurs locally as well; if an immediate neighbor has a higher score, a cell will adopt that neighbor's strategy. Within a spatialized and stochastic Prisoner's Dilemma, we've found, convergence is to a still higher level of generosity: a 'Bending over Backwards' or 'Forgiving Tit for Tat' <1-, 2/3> that returns cooperation with near-perfect cooperation but forgives defection with a probability of 2/3 (Grim 1995; Grim 1996; Grim, Mar, and St. Denis 1998).

Our attempt here is to borrow some of these formal tools from previous work on cooperation in order to construct a computer model for elementary forms of communication.

The question of perfect and imperfect worlds that has characterized research on cooperation is also one we want to carry over to the case of communication: how might communication evolve in stochastically perfect and imperfect worlds?

3. A Simple Model for Communication

Building on previous work, we again modeled our 'individuals' spatially as cells in a two-dimensional array.⁽⁴⁾ In the current model, however, there are no games of competition in the style of the Prisoner's Dilemma. Here we envisage instead a swarm of food sources moving across the spatial array, with individual cells gaining points by successfully feeding and losing points by failing to feed. In this model the behavioral repertoire of our cells also includes the ability to make a simple sound, which is heard locally by immediate neighbors and is potentially of use for purposes of communication. Each cell, acting in parallel, carries a strategy which specifies its behavior: when it will open its mouth for feeding, when it will make the one sound at its disposal, and how it will react to hearing a sound from its immediate neighbors.

Cells gain points by successfully feeding, and lose points by opening their mouths but failing to feed. After a number of generations each cell surveys its immediate neighbors. If any neighbor has a higher score, it converts to the most successful local strategy. Successful strategies can thus be expected to spread within the spatial array. Should communication prove a successful strategy, we should expect to see the spatial triumph of communicating communities spreading across the array.⁽⁵⁾

In somewhat more detail, the model is as follows. We use a randomized 64 x 64 two-dimensional cellular automata array of eight different strategies (Figure 2). Technically, the array forms a torus, 'wrapping around' so that individuals on the bottom edge have neighbors at the top edge, those at the left edge have neighbors on the right, etc. The cells themselves are thought of as stationary, something like coral in a reef. There are also, however, fifty bits of food that migrate in a random walk through the array.⁽⁶⁾ If a bit of food lands on a cell with its mouth open, that individual 'eats' and thus gains points. Our food sources were not eliminated or consumed, however: after an individual has 'eaten', that food source continues to migrate. A cell with an open mouth when no food is present loses some smaller number of points.

On each (synchronous) generation, each individual's strategy specifies its behavior with respect to sound and silence: whether it makes a sound audible by its immediate neighbors when it eats or not, whether it reacts to such a sound from its neighbors by opening or closing its mouth, and whether it reacts to silence from its neighbors by opening or closing its mouth. The strategies in this simple model can thus be conceived of as triplets <s, h, o>. The first variable s represents whether the individual makes a sound or not when it successfully feeds--when a food source has landed on its open mouth. The second variable h represents a reaction to hearing such a sound: whether a strategy opens its mouth in response to hearing a sound (from itself or its immediate neighbors) or not. The third variable o represents a reaction to hearing no sound: some strategies will open their mouths on the next generation when they heard no sound at all.

With three binary variables, we have a total of eight possible strategies:

<0,0,0> Makes no sound when feeding, never opens mouth

<0,0,1> Makes no sound when feeding, opens mouth only when it hears no sound

<0,1,0> Makes no sound when feeding, opens mouth when hears sound

<0,1,1> Makes no sound when feeding, mouth always open

<1,0,0> Sounds when feeding, never opens mouth

<1,0,1> Sounds when feeding, opens mouth when hears no sound

<1,1,0> Sounds when feeding, opens mouth when hears a sound, not otherwise

<1,1,1> Sounds when feeding, mouth always open

Fig. 2 Initial randomized array of 8 simple strategies. Communicators <1,1,0> are shown in white

Starting with a randomized array of our eight strategies, we run 100 generations of food migration, scoring for points gained or lost in feeding or missing food. After each such 'century' a subroutine is run, governing strategy change. At that point each cell compares its total score over the past 100 generations with each of its immediate neighbors. If any neighbor has a higher score, it switches to that strategy. If no neighbor has a higher score, it retains its original strategy.

The idea is thus an evolutionary competition between different strategies governing sounding and eating. Those strategies which prove more successful--and gain more points--can be expected to 'spread' as their surrounding neighbors converted to their strategy. Evolutionarily disadvantageous strategies can be expected to disappear.

4. The Failure of Communication in a Perfect World

What we were primarily concerned with was the prospect for 'communicating' strategies. Considered a priori, the prime communicator would appear to be the seventh strategy listed above: <1,1,0>. An individual with this strategy sounds when it eats and correspondingly reacts to sound by opening its mouth. A <1,1,0> individual who is successfully eating, then, will sound when doing so. Individuals in the immediate neighborhood who share the same strategy will open their mouths in response to that sound. Since the food item has a 1/9 possibility of migrating to each of those mouths in the next generation, each of those <1,1,0> neighbors will then have a 1/9 chance of eating on the next generation.⁽⁷⁾ If no sound is heard in the immediate neighborhood, on the other hand, <1,1,0> cells will keep their mouths closed, preventing them from the loss of points charged for a mouth open when no food is present.

The one detail we haven't yet specified is what values are to be assigned for the 'gain' of successful feeding and the loss of opening one's mouth but failing to feed. For what gain and loss will communication prove evolutionarily advantageous in such a model?⁽⁸⁾ Throughout our investigations we in fact used a 'loss' of 0.1; the question thus becomes what behavioral strategies would be favored given different sizes of 'gain' relative to this loss.

The surprising answer was that our 'communicator' strategy <1,1,0> took over in none of our runs.

For low gains-gains of 1 through 3, for example-<1,1,0> establishes a static equilibrium with strategies <0,0,0>, <0,1,0>, and <1,0,0>. All sound eventually ceases, and all four of these strategies remain with their mouths closed. As a result all get uniform scores of 0. No cell changes strategies in the subroutine, and the result is a frozen world occupied by several static strategies (Fig. 3a).

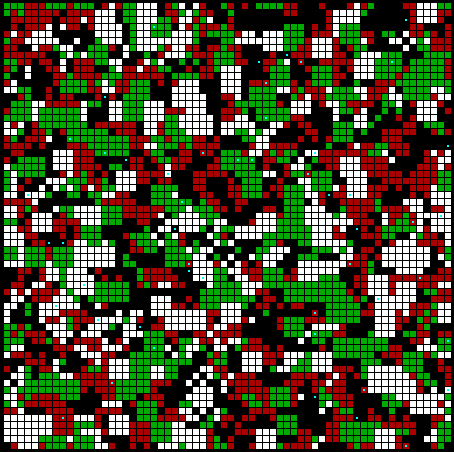
Fig 3a Gain 1 loss 0.1, with 'communicators' <1,1,0> shown in white: a static silent world.

At the high end of the scale-for a gain of 9, for example-the significant players are strategies <0,0,1> and <0,1,1>. One or the other of these, and sometimes a combination, generally occupy the bulk of the array. Some other single strategy may survive for a significant period in smaller islands, however- <0,0,0>, <0,1,0>, <1,0,0>, or our 'communicator' <1,1,0>. Here too, however, sound disappears quite quickly. Strategies in possession either have their mouths open all the time or closed all the time-our 'communicator' has no variable input of sound, and thus no variable output as a result. These are not static worlds, since territories of different strategies continue to shift. But from the point at which silence is reached, evolution of the array becomes simply a random matter of where food happens to fall, and thus of whether individuals with consistently open mouths get a better balance of 'gain' and 'loss' than the constant zero awarded to cells which never open their mouths (Figure 3c).

Fig 3b Gain 5, loss 0.1. A stage of silent but dynamic equilibrium between <0,0,1>,<0,1,1>(with open mouths), <1,1,0> (shown in white) and <0,1,0>.

Fig3c One possible evolution for gain 9, loss 0.1: a silent world dominated by <0,1,1> but with islands of <1,1,0>

That factor which correlated most clearly with relative gain, and the best predictor of array evolution, was time to silence. For gains 1 through 9 (that is, 10 to 90 times the value for a loss), all sound in the array eventually ceased. Since there were then no strategies on the board making sounds when fed, there was no longer any possibility for the selective reaction to sound characteristic of communication. The time to silence showed a clear increase with the ratio of gain to loss: for a gain of 1 silence was reached in about two centuries. For a gain of 4 it was reached in about 10 centuries. For gains of 5, 6, and 7 the time to silence was approximately 30, 35, and 45 centuries.

For low gains, favoring closed-mouthed strategies with uniform scores of 0, silent worlds are frozen worlds: all strategies have a uniform score of 0 and thus no 'conversion' takes place. For higher gains silent worlds need not be frozen: <0,0,1> and <0,1,1>, both of which sit in silence with their mouths open, continue to gain points in even a silent world, and random migration of food can result in change of territory. Not surprisingly, the higher the ratio of gain to loss the more quickly open-mouthed strategies occupy major parts of the array.

In no case, then, did our 'communicator' grow to occupy the entire array. Within the perfect world of this first model, communication did not have the advantage we hypothesized for it.

Why did our communicator <1,1,0> do so poorly? In retrospect, it seems clear that the communicators in this perfect world are disadvantaged by the fact that they cannot initiate successful communication. A <1,1,0> cell will respond to eating by making a sound heard by its neighbors. But it will open its mouth-the necessary prerequisite to eating-only if it hears a sound. Thus food items introduced into a uniform field of <1,1,0> would forever migrate uneaten: No-one would have heard the sound necessary to open their mouths, and thus no-one will have fed. If no-one has fed, no-one will make the sound necessary for others to open their mouths.

Consider therefore a cluster or community of <1,1,0> (among cells of other strategies) at some point in the development of this model. As long as a member of that community is successfully feeding, the food will continue to be eaten by its neighbors-one will be able to watch the food migrate across the cluster of cooperative strategies, always landing on an open mouth. Once the food migrates to a strategy which does not make a sound when it feeds, however, it can migrate back across the communicator cells without being eaten at all. At that point the <1,1,0> community has to hope for a neighbor who makes a sound, preferably when eating but possibly when not (giving the opportunity for a random 'feed'). In this first perfect world, communication does not have the evolutionary advantage we expected because our perfect communicators are literally non-starters. With external input they can continue a successful trail of feeding. But without it they cannot, since as perfect communicators in a perfect world they open their mouths only in reaction to sound, but sound only when feeding.

5. The Evolution of Communication in an Imperfect World

In our second series of trials we quite deliberately made our strategies less perfect by introducing a stochastic element in all third values o of our strategies <s, h, o>. Here we varied strategies1, 3, 5, and 7 above so as to allow a probability of 5% of open mouths even when no sound is heard. Strategies 2, 4, 6, and 8 are varied so as to allow a probability of 5% that they will close their mouths even when a sound is heard. All strategies, in other words, are made slightly imperfect in their reaction to sounds or silence. Following the work of Nowak and Sigmund regarding cooperation, our attempt in the second series of trials was to model an imperfect world for communication.

In this second model, then, a perfect strategy such as <0,0,1> is replaced with the imperfect variation <0,0,0.95>, which has a small probability of closing its mouth even when it hears no sound. Our perfect communicator <1,1,0> is replaced with the imperfect <1,1,0.05>, which has a small probability of opening its mouth and successfully feeding even if unprimed by sound.

In this stochastically imperfect world our results were emphatically in favor of communicators. For gains from 1 to 8, the 'communicator' strategy <1,1,0.05> eventually spread to cover the field in all cases (Figures 4a, 4b) . The time to conquest seemed to fluctuate, depending perhaps as much on random initial configuration as on the value assigned for gain. The following are results from a single series of runs: With a gain of 1 (as opposed to a loss of 0.1), the communicator <1,1,0.05> conquered in 83 centuries (scoring series based on 100 generations of play). With a gain of 2, it conquered in 117 centuries; with a gain of 3, in 129 centuries, and with a gain of 4 in 98. With a gain of 5, <1,1,0.05> conquered in 60 centuries, with a gain of 6 in 93, with a gain of 7 in 92, and with a gain of 8 in 84 centuries. A gain of 9 showed a victory for <1,1,0.05> as well, but only after 1,510 centuries.

Fig. 4a Conquest of 'communicator' with a gain of 5, loss 0.1, shown over 600 centuries

Fig. 4b Conquest of 'communicator' with a gain of 8, loss 0.1, shown over 600 centuries

For gains of 10 or greater, on the other hand, our communicative strategy was eliminated entirely (Figure 4c). Here evolution favored instead one or both strategies <0,0,0.95> or <0,1,0.95>, with the latter generally dominant. Neither <0,0,0.95> nor <0,1,0.95> makes any sound when feeding, and both open their mouths with a probability of 0.95 when they hear no sound. The only difference between them is that <0,1,0.95> opens its mouth and <0,0,0.95> closes its mouth when they hear a sound. Our cooperative <1,1,0.05> sounds when feeding, thereby benefitting both itself and neighboring <0,1,0.95>, but opens its mouth only on hearing a sound. In a neighborhood of dominant strategies <0,0,.95> or <0,1,.95>, then, our cooperator will avoid the -0.1 loss they pay for an unfed open mouth but will often go unfed in cases in which these other strategies feed--a food item will have migrated from an area of the other strategies without a warning sound. <1,1,0.05>'s advantage in avoiding loss for an open mouth unfed is thus paid for with a greater probability of failing to capture food with an open mouth. With an array of our size containing 50 food items, it turns out, a gain of 10 makes this trade-off disadvantageous and our communicators are extinguished as a result.

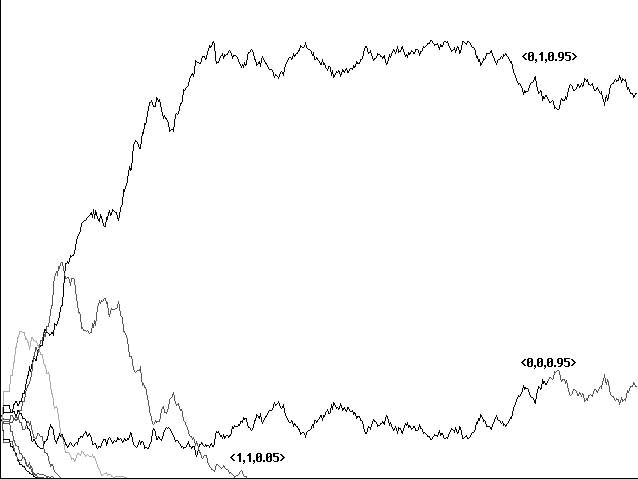
Fig. 4c 'Communicator' extinguished with a gain of 10, loss 0.1, shown over 600 centuries

How low can the gain be and still show an advantage for our communicator? In order to find out, we ran a further series of tests using gains of 0.1 through 0.9 against the standard loss of 0.1. Our 'communicator' <1,1,0.05> was eliminated entirely for gains of 0.6 or lower: strategies <0,0,0.05>, <0,1,0.05>, and <1,0,0.05> tended to hold the field entirely, with no communication and scores tending to zero throughout. For a gain of 0.8, on the other hand, <1,1,0.05> might conquer the entire field at 237 centuries, and for a gain of 0.9 at might conquer after 137 centuries. A gain of 0.7 seemed to mark a very extended competition, going eventually to our 'communicator', but only after a number of centuries that varied from 500 to 1000 (Figures 5a and 5b).

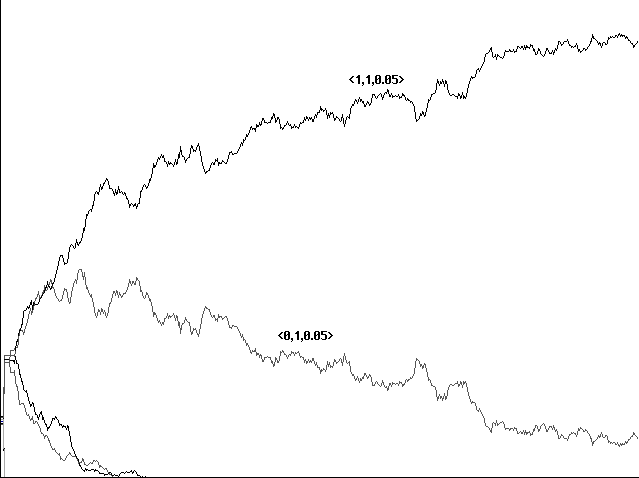
Fig. 5a Rocky evolution toward communication with a gain of 0.7, loss 0.1, shown over 600 centuries

Fig. 5b Conquest by communication with a gain of 0.9, loss 0.1, shown over 600 centuries

6. Conclusion

What these simple models seem to indicate is that communication proves to be an evolutionary advantage only in a world that is not communicatively perfect. For communication to flourish, advantaged responses such as opening one's mouth must also happen independently of receipt of a communicative message, even if they happen only randomly. If all action depends on communication, the benefits of communication disappear.

We think these results tie in quite nicely with the earlier work on cooperation in perfect and imperfect worlds. Nowak and Sigmund's work has made it clear that an imperfect world favors greater cooperation in the iterated Prisoner's Dilemma. The work above indicates that an imperfect world is required in order to advantage simple forms of communication as well. These two classes of models are very different in a number of regards, of course-here the competition of the Prisoner's Dilemma plays no role, for example. Nonetheless the general conclusion that an imperfect world favors communication as it does cooperation should perhaps have been expected. Communication is, after all, a particular form of cooperation.

References

Ackley, D., and Littman, M., 1994. Altruism in the Evolution of Communication. In Rodney A. Brooks and Pattie Maes, eds., Artificial Life IV: Proceedings of the Fourth International Workshop on the Synthesis and Simulation of Living Systems (MIT Press), 40-48.

Axelrod, R. 1980a, Effective choice in the Prisoner's Dilemma. J. Conf. Resolut. 24, 3-25.

Axelrod, R., 1980b, More effective choice in the Prisoner's Dilemma. J. Conf. Resolut. 24, 379-403.

Axelrod, R., 1984, The Evolution of Cooperation (Basic Books, New York).

Axelrod, R., 1985, The emergence of cooperation among egoists. In T. Campbell and L. Sowden, eds., Paradoxes of Rationality and Cooperation (Univ. Of British Columbia Press, Vancouver).

Axelrod, R., and Hamilton, W., 1981, The evolution of cooperation. Science 211, 1390-1396.

Grim, P. 1995. Greater generosity in the spatialized Prisoner's Dilemma. J. Theo. Bio. 173, 353-359.

Grim, P. 1996. Spatialization and greater generosity in the stochastic Prisoner's Dilemma. BioSystems 37, 3-17.

Grim, P., Mar, G., and St. Denis, P., 1998. The Philosophical Computer: Exploratory Essays in Philosophical Computer Modeling (MIT Press/Bradford Books)

Lewis, David, 1969. Convention (Harvard University Press, Cambridge MA)

Maclennan, B., 1991. Synthetic Ethology: An approach to the study of communication. In C. G. Langton, C. Taylor, J. D. Farmer, and S. Rasmussen, eds., Artificial Life II, SFI Studies in the Sciences of Complexity, vol. X (Addison-Wesley), 631-655.

Nowak, M., and Sigmund, K., 1990. The evolution of stochastic strategies in the prisoner's dilemma. Acta Applicandae Mathematicae 20, 247-265.

Nowak, M. and Sigmund, K., 1992, Tit for tat in heterogeneous populations. Nature 355, 250-252.

Sigmund, K., 1993. Games of Life (Oxford University Press, New York).

Skyrms, B., 1996. Evolution of the Social Contract (Cambridge University Press, New York).

Werner, G., and Dyer, M., 1991. Evolution of Communication in Artificial Organisms. In C. G. Langton, C. Taylor, J. D. Farmer, and S. Rasmuseen, eds., Artificial Life II, SFI Studies in the Sciences of Complexity, vol. X (Addison-Wesley), 659-687.

Notes

1. Opposition to the classical approach might be characterized as Wittgensteinian, though that may also be where our affinities with Wittgenstein end.

2. In the round-robin tournaments each strategy was pitted against every other, plus itself and a single 'strategy' producing a random series of plays. The winner was that strategy with the most points over all.

3. In Nowak and Sigmund's work, unlike Axelrod's, the model is built in terms of a mathematical fiction of an infinitely iterated game. Given stochastically imperfect strategies, an infinite series of games will swamp the effect of any initial play, and strategies can therefore be specified without mention of the initial move. See Grim 1995, 1996.

4. All software is available by request from the authors.

5. There are very few previous models for communication of the sort we outline here. MacLennan 1991 proposes a model in which 'senders' and 'receivers' are both rewarded in cases of successful communication involving arbitrary symbols, and in which communicative strategies are perfected through the application of a genetic algorithm. A major limitation of the model is that communication in no way arises 'naturally': communicative matches are judged from the outside, as it were, and not only those receiving the message but those sending it are rewarded from the outside when a match is made. As Ackley and Littman 1994 note, the result is an arrtificial situation "where 'truthful speech' by a speaker and 'right action' by a listener causes food to rain down on both."

Werner and Dyer 1991 introduce a feature that our model shares--a spatially distributed population. Their model is limited to communication which facilitates reproduction by allowing 'males' and 'females' to find each other more rapidly, however, and the fact that a globally-mixing rather than a local reproductive strategy is used seems to limit the benefits of spatialization. Here again, moreover, communication is modeled as a process which somehow rewards both sender and receiver simultaneously.

Ackley and Littman 1994 attempt to improve on these earlier attempts by studying the evolution of communication in at least a limited spatial environment and in response to food and predators-a construction which rewards communication only indirectly as it contributes to successful feeding and avoidance of harm. Ackley and Littman immediately complicate their model, however, with a blizzard of interacting factors: individual, local and global organizational levels, scoring and processing in different ways at different points, a distinction between genotype and phenotype, the complications of 32-unit neural nets coded with both synaptic specification genes and pseudo-genes which are processed by genetic algorithm, and finally reproductive festivals declared at official holidays and a peculiar wind-driven diffusion. We consider Ackley and Littman's work a warning against over-ambitious and baroque model building: their conclusions prove difficult to interpret precisely because the model itself is so unnecessarily over-complicated.

In terms of general approach rather than model details, the closest philosophical ancestor of our work is that of Bryan Skyrms 1996, itself a sophisticated response to David Lewis's groundbreaking work in Lewis 1969.

6. For each of 50 food items, our programming chose initial random numbers between 1 and 64 for each axis on the 64 x 64 array. Thus it is possible that less than 50 cells originally contained food items. At each generation each food item randomly 'walked' 0 or 1 cell in each direction, again with the result that less than 50 cells might contain food items at any one generation. In general the number of cells containing food items on any one generation was approximately 49.

7. Because of the complication noted in note 1, this can be taken as only a rough probability: there is a small probability that there may be two food items 'superimposed' on a cell that is feeding, in which case the probability of a surrounding cell being fed on the next generation will be significantly greater than 1/9.

8. One can easily calculate that point at which a uniformly open mouth is of equal value to a uniformly closed mouth in such a model. Where f is the number of food particles, n is the number of cells, g is our gain and l is our loss, the breakpoint will be:

fg + (n-f)l = 0

For fifty food items, a display of 64 x 64 cells, and a loss of 0.1, the breakpoint for our gain is approximately 8.09. At a gain greater than that, universally open mouths are advantaged over closed mouths. At a gain lower than that, universally closed mouths have the advantage.

The reason this is not the whole of the story, of course, is that we have a varied population of cells with more sophisticated repertoires than merely open and closed mouths. The results below indicate that communication significantly complicates the picture.