
Fig. 17
The rug enumeration patterns offered above are perhaps the most direct way to attempt to model a complete formal system in terms of the values of its wffs. There is one major respect in which these patterns do not correspond to the fractal outlined for tic-tac-toe in introduction, however. That fractal is deep: all tic-tac-toe games are contained within the large initial square, though at decreasing scale. The rug patterns offered above, on the other hand, are not in principle exhibitable in a finite space: all occupy an infinite plane extending without limit to the right and bottom.
It is also possible, however, to outline fractals for at least simple systems of propositional calculus which are deep in the sense of the tic-tac-toe game. In the case of systems with infinite wffs, of course, the corresponding fractal must be infinitely deep.

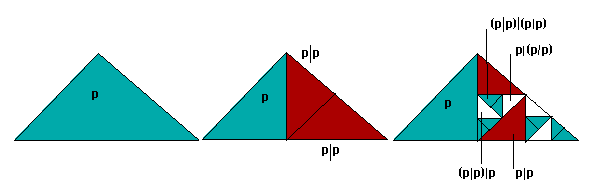
At the next step we take each of the new triangles thus created, divide half of their space into two, and embed in each of these smaller triangles an appropriately colored image of the whole--representing Sheffer stroke formulae (a|b) of the present formulae over all previous formulae and Sheffer stroke formulae (b|a) of all previous formulae over the present.
At each step a new set of more complex formulae are created, and at each step all Sheffer stroke combinations of elements of this new set with all previous formulae are embedded in the total image. Tautologies are colored white, as before, and contradictions black. All formulae of our simple formal system are thus represented with their value colors somewhere in the infinite depths of the fractal. Indeed many are represented redundantly--(p|p) appears twice at the first step, for example (representing the present formula p over the previous formula p and vice versa), and later complexes with (p|p) on either side will carry the redundancy further. The complete fractal represents propositional calculus formulated in terms of the Sheffer stroke for a single sentence letter as a whole, infinitely embedded on the model of the tic-tac-toe fractal with which we began.
Modelling in terms of theorem fractals can be extended to more than a single sentence letter by starting with a larger number of initial areas: an initial triangle with two major divisions for p and q, for example, with three for p, q, and r, and so forth. Any of these could then be subdivided precisely as before, once again embedding the whole image into each subdivision. If we wish, we can even envisage an initial triangle with room for infinitely many sentence letters arranged Zeno-style in infinitely smaller areas. The embedding procedure would proceed as before, though of course each embedding would involve the mirroring of infinitely many areas into infinitely many. We haven't yet tried to extend such a pattern to quantification.